Thiết kế và đánh giá thuật toán

Như đã biết, tính của ma trận A = (a_ik) kích thước p x q với ma trận B = (b_kj) kích thước q x r là ma trận C = (c_ij) kích thước p x r với các phần tử được tính theo công thức:

$c_{\text{ij}}=\sum _{k=1}^q{a}_{\text{ik}}{b}_{\text{ki}},$1 ≤ i ≤ p, 1 ≤ j ≤ q.

Chúng ta có thể sử dụng đoạn chương trình sau đây để tính tích của hai ma trận A,B:

for i =1 -> p

for j =1 -> r

{

c [i,j] = 0

for k = 1 -> q do

c[i,j] =c[i,j] +a[i,k] *b[k,j];

}

Rõ ràng , đoạn chương trình trên đòi hỏi thực hiện tât cả pqr phép nhân để tính tích của hai ma trận.

Giả sử ta phải tích tích của nhiều hơn là hai ma trận. Do phép nhân ma trận có tính kết hợp, ta có thể tích tích của các ma trận.

M = M₁M₂…Mn

Theo nhiều cách khác nhau, chẳng hạn

M =(…((M₁M₂)M₃)…Mn)

= (M1(M₂(M₃…(Mn_-1Mn)…)))

=(…((M₁M₂)(M₃M₄))…),v.v…

Mặt khác, do tích ma trận không có tính chất giao hoán, nên ta không được thay đổi thứ tự của các ma trận trong biểu thức đã cho.

Mỗi cách tính tích các ma trận đó cho đòi hổi một thời gian tính khác nhau. Để đánh giá hiệu quả của các phương pháp chúng ta đếm số phép nhân cần phải thực hiện. Trong đoạn chương trình trên, ta thấy để tính tích của hai ma trận ta còn phải thực hiện cùng một số như vậy các phép cộng và một số phép gán và tính chỉ số, vì thế, số lượng phép nhân là một chỉ số đánh giá khá chính xác hiệu quả của phương pháp.

Ví dụ: Tính tích M = ABCD của bốn ma trận, trong đó A có kích thước 13 x 5, B có kích thước 5 x 89, C có kích thước 89 x 3 và D có kích thước 3 x 34. Sử dụng cách tính

M = ((AB)C)D),

Ta phải thực hiện lần lượt tính

AB 5785 phép nhân

(AB)C 3271 phép nhân

((AB)C)D 1326 phép nhân

Và tổng cộng là 10582 phép nhân

Tất cả có 5 phương pháp khác nhau để tính tích ABCD:

1. ((AB)C)D 10582

2. (AB)(CD) 54201

3. (A(BC))D 2856

4. A((BC)D) 4055

5. A(B(CD)) 26418

Phương pháp hiệu quả nhất (phương pháp 3) đòi hỏi khối lượng phép nhân ít hơn gần 19 lần so với phương pháp tồi nhất (phương pháp 5).

Để tìm phương pháp hiệu quả nhất, chúng ta có thể liệt kê tất cả các cách điền dấu ngoặc vào biểu thức tích ma trận đã cho và tính số lượng phép nhân đòi hỏi theo mỗi cách. Ký hiệu T (n) là số cách điền các dấu ngoặc vào biểu thức tích của n ma trận. Giả sử ta định đặt dấu ngoặc phân tách đầu tiên vào giữa ma trận thứ i và ma trận thứ (i + 1) trong biểu thức tích, tức là:

M = (M₁ M₂ … Mi)(Mi₊₁ Mi₊₂ … Mn)

Khi đó có T(i) cách đặt dấu ngoặc cho thừa số thứ nhất (M₁ M₂ … Mi) và T(n-i) cách đặt dấu ngoặc cho thừa số thứ hai (Mi₊₁ Mi₊₂ … Mn) và từ đó T(i)T(n-i) cách tính biểu thức (M₁ M₂ … Mi)(Mi₊₁ Mi₊₂ … Mn). Do i có thể nhận bất cứ giá trị nào trong khoảng từ 1 đến n-1, suy ra ta có công thức truy hồi sau để tính T(n):

Kết hợp với điều kiện đầu hiển nhiên T(1) = 1, ta có thể tính các giá trị của T(n) với mọi n. Bảng dưới đây cho một số giá trị của T(n).

Giá trị của T(n) được gọi là số Catalan. Công thức sau đây cho phép tính T(n) qua hệ số tổ hợp:

$T(n)=\frac{1}{n}{C}_{\mathrm{2n}-2}^{n-1},$ n ≥ 2

Từ đó T(n) = T(n) = 4ⁿⁿ². Như vậy, phương pháp duyệt toàn bộ không thể sử dụng để tìm cách tính hiệu quả biểu thức tính của n ma trận, khi n lớn.

Bây giờ, ta xét cách áp dụng quy hoạch động để giải bài toán đặt ra.

* Phân rã (Xác định cấu trúc con tối ưu).

Bước đầu tiên phải thực hiện khi muốn áp dụng quy hoạch động để giải bài toán đặt ra là tiến hành phân rã bài toán hay phát hiện cấu trúc con tối ưu. Nhận thấy rằng: Nếu cách tính tối ưu tích của n ma trận đòi hỏi dặt dấu ngoặc tách đầu tiên giữa ma trận thứ i và thứ (i+1) của biểu thức tích, thì khi đó cả hai tích con (M₁ M₂ … Mi) và (Mi₊₁ Mi₊₂ … Mn) cũng phải được tính một cách tối ưu. Khi đó số phép nhân cần phải thực hiện để nhân dãy ma trận sẽ bằng tổng số phép nhân cần thực hiện để nhân hai dãy con ((M₁ M₂ … Mi) và (Mi₊₁ Mi₊₂ … Mn) cộng với số phép nhân cần thực hiện để nhân hai ma trận kết quả tương ứng với hai dãy con này. Vì vậy để xác định cách thực hiện nhân tối ưu ta cần giải quyết hai vấn đề sau:

- Cần đặt dấu ngoặc phân tách đầu tiên vào vị trí nào (xác định i);

- Thực hiện việc tính tối ưu hai tích con (M₁ M₂ … Mi) và (Mi₊₁ Mi₊₂ … Mn) bằng cách nào.

Việc tính mỗi tích con rõ ràng có dạng giống như bài toán ban đầu, vì thế có thể giải một cách đệ quy bằng cách áp dụng cách giải như đối với dãy xuất phát. Vấn đề thứ nhất có thể được giải bằng cách xét tất cả các giá trị có thể của i. Như vậy, bài toán nhân dãy ma trận thoả mãn đòi hỏi về cấu trúc con tối ưu: Để tìm cách tính tối ưu việc nhân dãy ma trận (M₁ M₂ .. M_n) chúng ta có thể sử dụng cách tính tối ưu của hai tích con (M₁ M₂ … Mi) và (Mi₊₁ Mi₊₂ … Mn). Nói cách khác, những bài toán con phải được giải một cách tối ưu cũng như bài toán ban đầu. Phân tích này cho phép ta sử dụng quy hoạch động để giải bài toán đặt ra. Xét họ các bài toán:

Tìm m_ij là số phép nhân ít nhất cần thực hiện để tính tích

(Mi₊₁ Mi₊₂ … Mj), 1 ≤ i ≤ j ≤ n

Lời giải cần tìm sẽ là m_1n

* Tổng hợp lời giải.

Giả sử kích thước của các ma trận được cho bởi véc tơ d[0 … n], trong đó ma trận Mi có kích thước di_-1xdi, i = 1, 2, 3, … n. Ta sẽ xây dựng bảng giá trị mi j lần lượt theo từng đường chéo của nó, trong đó đường chéo thứ s chứa các phần tử mi j với chỉ số thoả mãn j - i = s. Khi đó, đường chéo s = 0 sẽ chứa các phần tử mi _j (i = 1, 2, … n) tương ứng với tích có một phần tử Mi. Do đó, mi _j = 0, i = 1, 2, … n. Đường chéo s = 1 chứa các phần tử m_ij+1 tương ứng với tích M_iM_{i + 1}, do ở đây không có sự lựa chọn nào khác, nên ta phải thực hiện d_{i - 1}d_id_{i + 1} phép nhân. Giả sử s > 1, khi đó đường chéo thứ s chứa các phần tử mij+s tương ứng với tích Mi Mi+1 … Mi+s. Bây giờ ta có thể lựa chọn việc đặt dấu ngoặc tách đầu tiên sau một trong số các ma trận Mi, Mi+1, …, Mi+s-1. Nếu đặt dấu ngoặc đầu tiên sau Mk, i ≤ k < i+s , ta cần thực hiện mik phép nhân để tính thừa số thứ nhất, mk+1,i+s phép nhân để tính thừa số thứ hai, và cuối cùng là di-1dkdi+s phép nhân để tính tích của hai ma trận thừa số để thu được ma trận kết quả. Để tìm cách tính tối ưu, ta cần chọn cách đặt dấu ngoặc tách đòi hỏi ít phép nhân nhất.

Như vậy, để tính bảng giá trị mi j ta có thể sử dụng quy tắc sau đây:

s = 0; mi _j = 0 i = 1, 2, …, n

s = 1; mi _{j + 1} = di_–1didi₊₁, i = 1, 2, …, n - 1

1 < s < n; mi _j+s = min{mik + mk_{+1, i+s} + di_-1dkdi_+s: 1 ≤ k < i+s}, i = 1, 2, …, n – s.

Lưu ý rằng, để dễ theo dõi ta viết cả công thức cho trường hợp s = 1, mà dễ thấy là công thức cho trường hợp tổng quát vẫn đúng cho s = 1.

Ví dụ 2: Tìm cách tính tối ưu cho tích của bốn ma trận cho trong ví dụ 1.

Ta có d = (13, 5, 89, 3, 34). Với s = 1, m12 = 5785, m23 = 1335 và m34 = 9078. Tiếp theo, với s = 2 ta thu được

m₁₃ = min(m₁₁ + m₂₃ + 13 x 5 x 3, m₁₂ + m₃₃ + 13 x 89 x 3)

= min(1530, 9256) = 1530

m₂₄ = min(m₂₂ + m₃₄ + 5 x 89 x 34, m₂₃ + m₄₄ + 5 x 3 x 34)

= min(24208, 1845) = 1845

Cuối cùng với s = 3 ta có

m₁₄ = min(m₁₁ + m₂₄ + 13 x 5 x 34), {k = 1}

m₁₂ + m₃₄ + 13 x 89 x 34, {k = 2}

m₁₃ + m₄₄ + 13 x 3 x 34, {k = 3}

= min(4055, 54201, 2856) = 2856.

Bảng giá trị m được cho trong hình vẽ dưới đây

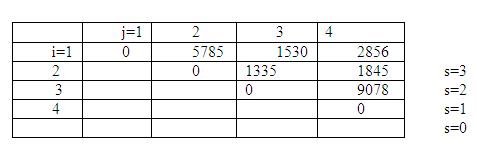
Để tìm lời giải tối ưu, ta sử dụng bảng hi j ghi nhận cách đặt dấu ngoặc tách đầu tiên cho giá trị mi j.

Ví dụ 3: Các giá trị của hi j theo ví dụ 1 được cho trong bảng dưới đây:

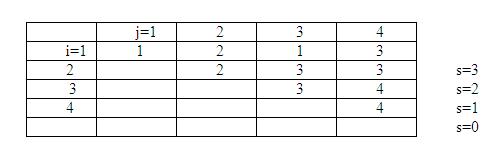
Ta có số phép nhân cần thực hiện là m14 = 2856. Dấu ngoặc đầu tiên cần đặt sau vị trí h14 = 3, tức là M = (ABC)D. Ta tìm cách đặt dấu ngoặc đầu tiên để có m13 tương ứng với tích ABC. Ta có h13 = 1, tức là tích ABC được tính tối ưu theo cách: ABC = A(BC). Từ đó suy ra, lời giải tối ưu là: M = (A(BC))D.

Bây giờ, ta tính số phép toán cần thực hiện theo thuật toán vừa trình bày. Với mỗi s > 0, có n – s phần tử trên đường chéo cần tính, để tính mỗi phần tử đó ta cần so sánh s giá trị số tương ứng với các giá trị có thể của k. Từ đó suy ra số phép toán cần thực hiện theo thuật toán là cỡ

$\begin{array}{}\sum _{s=1}^{n-1}\left(n-s\right)s=n\sum _{s=1}^{n-1}s-\sum _{s=1}^{n-1}{s}^2\\ n^2\left(n-1\right)/2-n\left(n-1\right)\left(\mathrm{2n}-1\right)/6\\ \left(n^3-n\right)/6\\ 0\left(n^3\right)\end{array}$

Thuật toán trình bày có thể mô tả trong hai thủ tục sau:

procedure Matrix-Chain(d,n)

{m[i,j] - chi phí tối ưu thực hiện nhân dãy Mi . . . Mj;

h[i,j] - ghi nhận vị trí đặt dấu ngoặc đầu tiên trong cách thực hiện nhân dãy Mi . . . Mj}

begin

for i: = 1 to n do m[i,j]: = 0; //khởi tạo

for s: = 1 to n do // s = chỉ số của đường chéo

for i: = 1 to n - s do

begin

j: = i + s - 1; m[i,j] = +?;

for k: = i to j - 1 do

begin

q: = m[i,k] + m[k+1,j] + d[i-1]*d[k]*d[j];

if(q<m[i,j]) then

begin

m[i,j] = q; h[i,j] = k;

end;

end;

end;

end;

Thủ tục đệ quy sau đây sử dụng mảng ghi nhận h để đưa ra trình tự nhân tối ưu.

procedure Mult(i,j);

begin

if(i<j) then

begin

k = h[i,j];

X = Mult(i,k); { X = M[i] / . . . M[k] }

Y = Mult(k+1,j); { Y = M[k+1] . . . M[j] }

return X*Y; { Nhân ma trận X và Y }

end

else

return M[i];

end;