Phương pháp sử dụng định luật Bio-Xavar-Laplax

Theo quan điểm của phương pháp này lực điện động là kết quả tương tác lẫn nhau của dây dẫn l mang dòng điện I và từ trường do dây dẫn khác tạo nên.

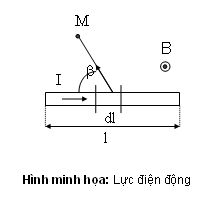
- Lực điện động tác dụng lên chiều dài l khi có dòng điện I đặt trong từ trường có từ cảm $\overrightarrow{B}$ là:

$\overrightarrow{\mathrm{\Delta F}}=I\text{.}\overrightarrow{\mathrm{\Delta l}}x\overrightarrow{\mathrm{\Delta B}}\begin{array}{cc}& \end{array}\text{hay}\begin{array}{cc}& \end{array}\mid \overrightarrow{\mathrm{\Delta F}}\mid =I\text{.}B\text{.}\mathrm{\Delta l}\text{.}\text{sin}\alpha$

Với góc  là góc hợp bởi $\overrightarrow{\mathrm{\Delta l}}$ và $\overrightarrow{B}$ ( $\overrightarrow{\mathrm{\Delta l}}$cùng chiều $\overrightarrow{I}$).

 là góc xác định theo chiều quay nhỏ nhất.

- Dạng vi phân là $d\overrightarrow{F}=I\text{.}d\overrightarrow{l}x\overrightarrow{B}$

$\mid d\overrightarrow{F}\mid =I\text{.}B\text{.}\text{dl}\text{.}\text{sin}\alpha$ (4-1)

Có : $\overrightarrow{\text{dl}}$trùng chiều dòng điện i.

Từ đó ta có lực điện động :

$\mid \overrightarrow{F}\mid =\underset{0}{\overset{l}{\int }}\mid d\overrightarrow{F}\mid =\underset{0}{\overset{l}{\int }}I\text{.}\text{Bdl}\text{sin}\alpha$= I.B. l. $\text{sin}\alpha$ (4-2)

- Nếu hai dây dẫn cùng trong một mặt phẳng  = 900 thì $F=\underset{0}{\overset{l}{\int }}\text{IBdl}$=I.B.l.

Muốn xác định được F ta phải tìm được quan hệ B = B(l), cảm ứng từ phụ thuộc kích thước dây dẫn.

- Theo Bio-Xavar-Laplax thì cường độ từ cảm tại một điểm M $\overrightarrow{B}$ có trị số là :

$\overrightarrow{B}=\frac{{\mu }_0}{\mathrm{4\pi }}I\int \frac{d\overrightarrow{l}x\overrightarrow{r_0}}{r^2}\text{, hay}\mid \overrightarrow{B}\mid =\frac{{\mu }_0}{\mathrm{4\pi }}I\int \frac{\text{dl}\text{.}\text{sin}\beta }{r^2}$ (4-3)

Trong đó:

$\begin{array}{}\overrightarrow{r_0}\text{laì veïctå âån vë choün tæì dl âãún M coï}\mid \overrightarrow{r_0}\mid =1\\ r:\text{laì khoaíng caïch tæì dl âãún M}\text{.}\\ \beta \text{: goïc håüp båíi d}\overrightarrow{l}\text{vaì}\overrightarrow{r_0}\\ \overrightarrow{B}\text{: veïc tå caím æïng tæì thàóng goïc våïi màût phàóng}\\ \text{do d}\overrightarrow{l}\text{vaì}\overrightarrow{r_0}\text{taûo lãn}\text{.}\\ \\ \\ \\ \begin{array}{}\{\{\{\{\end{array}\\ \end{array}$

Phương pháp cân bằng năng lượng

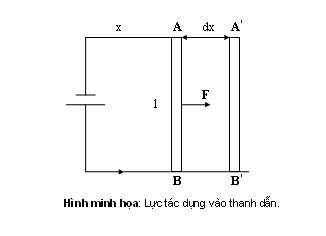
Xét một dây dẫn có dòng điện chạy qua như hình minh họa trên. Khi dây dẫn dịch chuyển theo hướng x một đoạn dx thì lực điện động được xác định bởi :

dw = F.dx $\Rightarrow \begin{array}{cc}& F=\frac{\text{dw}}{\text{dx}}\end{array}$ (4-4)

Trong đó:

+ dw : độ biến thiên năng lượng từ trường của vật dẫn mang dòng điện khi di chuyển một đoạn dx.

+ x : phương chuyển dời có thể có của dây dẫn dưới tác dụng của lực F.

+ Chiều $\overrightarrow{F}$ trùng với chiều dx.

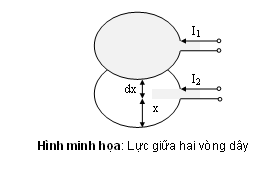
Ví dụ: xét hệ hai vật dẫn mang hai dòng điện i1 ; i2 như hình minh họa trên đặt song song cách nhau một khoảng x. Năng lượng từ trường của hệ là:

$\begin{array}{}\\ W_M=\frac{1}{2}{L}_1{i}_1^2+\frac{1}{2}{L}_2{i}_2^2+{\text{Mi}}_1{i}_2\text{vaì}\text{læûc taïc duûng laì :}\\ F=\frac{{\text{dw}}_M}{\text{dx}}=\frac{d\frac{1}{2}{L}_1{i}_1^2+\frac{1}{2}{L}_2{i}_2^2+{\text{Mi}}_1{i}_2}{\text{dx}}\\ \text{Ta coï læûc taïc duûng riãng reî seî laì :}\\ F_1=\frac{1}{2}{i}_1^2\text{.}\frac{{\text{dL}}_1}{\text{dx}}[J/\text{cm}]\\ F_2=\frac{1}{2}{i}_2^2\text{.}\frac{{\text{dL}}_2}{\text{dx}}[J/\text{cm}]\\ \\ \\ \begin{array}{}\\ \\ \\ \begin{array}{}\{\end{array}\\ \end{array}\\ \end{array}$

Khi vật thể biến dạng hoặc chuyển dời ta giả thiết các dòng điện bằng hằng số. Theo phương pháp này muốn tính lực ta phải biết được biểu thức toán học của hệ số tự cảm L và hỗ cảm M theo x. Các phương pháp tính L và M nêu trong giáo trình lí thuyết trường điện từ.

Ứ́ng dụng phương pháp cân bằng năng lượng

Ta xét lực điện động trong một số trường hợp vật dẫn đồng nhất nằm trong từ trường đều. Các trường hợp khác có thể tham khảo tài liệu chuyên ngành chế tạo thiết bị.

1. Lực điện động tác dụng lên một vòng dây có dòng i nằm trong một từ trường

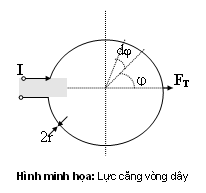
Giả thiết bán kính vòng dây R, bán kính dây dẫn r (hình minh họa). Lực điện động có xu hướng kéo căng vòng dây dẫn bung ra. Giả thiết lực phân bố đều trên chu vi vòng dây. Gọi fR là lực tác dụng lên một đơn vị dài chu vi theo hướng kính, lực tác dụng tổng: $F=\mathrm{2\pi }\text{.}R\text{.}{f}_R=\frac{1}{2}{I}^2\text{.}\frac{\text{dL}}{\text{dR}}$ (4-6)

Theo Kiếc khốp có: $L={\mu }_{0}R\text{ln}\frac{\mathrm{8R}}{r}-\mathrm{1,}\text{75}$.

Và ta giả thiết thay vào biểu thức (4-6) ta có:

$F=\frac{1}{2}{\mu }_0\text{.}{I}^2\text{ln}\frac{\mathrm{8R}}{r}-\mathrm{0,}\text{75}\text{biãút}{\mu }_0=\mathrm{0,4}\text{.}\prod \text{.}{\text{10}}^{-8}\left[\frac{H}{m}\right]$

Vậy $F=\mathrm{2,}\text{04}\text{.}\pi \text{.}{\text{10}}^{-8}\text{.}{I}^2\text{ln}\frac{\mathrm{8R}}{r}-\mathrm{0,}\text{75}\begin{array}{cc}& \end{array}[\text{kg}]$ (4-7)

Để tính độ bền cơ khí vòng dây, ta phải xác định lực có xu hướng kéo đứt vòng dây theo hướng kính (là tích phân hình chiếu các lực hướng kính tác dụng lên 1/4vòng dây) là :

$F_R=\underset{0}{\overset{\frac{\pi }{2}}{\int }}{f}_R\text{.}R\text{.}\text{cos}\varphi \text{.}\mathrm{d\varphi }=f_R\text{.}R={\text{10}}^{-7}\text{.}{I}^2\text{ln}\frac{\mathrm{8R}}{r}-\mathrm{0,}\text{75}$N

* Trong trường hợp cuộn dây có W vòng, thay IW cho I, ta có :

$F_R={\text{10}}^{-7}\text{.}(\text{WI}{)}^2\text{ln}\frac{\mathrm{8R}}{r}-\mathrm{0,}\text{75}[N]=\mathrm{1,}\text{02}\text{.}{\text{10}}^{-8}\text{.}(\text{WI}{)}^2\text{ln}\frac{\mathrm{8R}}{r}-\mathrm{0,}\text{75}[\text{kg}]\text{.}$ (4.9)

Chú ý: 1[N]=0,102 [kg] và 1[J/cm]=10,2[kg].

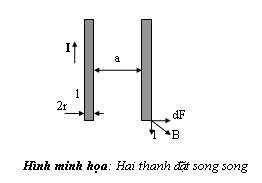
b) Tính lực điện động giữa hai dây dẫn tiết diện tròn đặt song song mang dòng i

Ta sử dụng phương pháp cân bằng năng lượng với giả thiết hai dây dẫn có bán kính r đặt song song cách nhau khoảng a.

Ta biết theo lí thuyết trường đối với dây dẫn như trên thì hệ số tự cảm là :

$L=\frac{{\mu }_{0\text{.}}l}{\mathrm{2\pi }}\frac{1}{2}+2\text{.}\text{ln}\frac{a-r}{r}$

Với: l là chiều dài của dây dẫn.

Lực tác dụng vào từng thanh dẫn được tính:

$F=\frac{{\text{dW}}_M}{\text{da}}=\frac{I^2\text{.}\text{dl}}{2\text{da}}=\mathrm{0,2}\text{.}{\text{10}}^{-8}\text{.}{I}^2\text{.}\frac{l}{a-r}$ [J/cm]. (4.10)

Nếu có a>>r thì:

$F=\mathrm{2,}\text{04}\text{.}{\text{10}}^{-8}\text{.}{I}^2\text{.}\frac{l}{a}$ [kg] (4.11)

Nếu dòng trong hai dây cùng chiều thì hai dây dẫn sẽ hút

nhau và ngược chiều thì đẩy nhau.

Ứng dụng định luật Bio-Xavar-Laplax

a) Lực điện động tác dụng lên hai dây dẫn đặt trong cùng một mặt phẳng

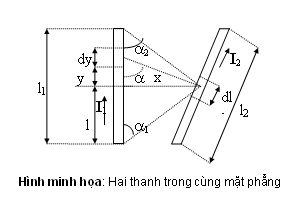
Trên hình minh họa là hai dây dẫn l1 và l2 cùng đặt trong một mặt phẳng. Dây dẫn l1 mang dòng I1 dây dẫn l2 mang dòng I2.

Ta tìm sự phân bố lực lên dây dẫn l2.

Ta chọn trục tung oy trùng với dây l1 (chọn hệ xoy hình 4-6). Dòng I1 ở đơn vị dy trong dây l1 tạo ra ở đoạn dl có cường độ từ cảm là :

$d\overrightarrow{B}=\frac{{\mu }_0}{\mathrm{4\pi }}{I}_1\frac{d\overrightarrow{y}x{\overrightarrow{r}}_0}{r^2}$ hay:

$\text{dB}=\frac{{\mu }_0}{\mathrm{4\pi }}{I}_1\text{dy}\frac{\text{sin}(\pi -\alpha )}{r^2}$

Vì có: sin( $p-\alpha$)= sin $\alpha$ nên:

$\text{dB}=\frac{{\mu }_0}{\mathrm{4\pi }}{I}_1\text{dy}\frac{\text{sin}\alpha }{r^2}$

Lực tác dụng lên đoạn dl2 do I1dy gây ra là:

$d\overrightarrow{F}=I_2\text{.}d{\overrightarrow{l}}_{2}xd\overrightarrow{B}$

Hay:

$\text{dB}=\frac{{\mu }_0}{\mathrm{4\pi }}{I}_1{I}_2\text{dy}\text{.}{\text{dl}}_2\frac{\text{sin}\alpha }{r^2}\text{.}\text{sin}{\text{90}}^0$

$$Từ hình 4-6 ta có :

y=cotg $\alpha ;\text{dy}=\frac{-x}{{\text{sin}}^2\alpha }\mathrm{d\alpha };r=\frac{x}{\text{sin}\alpha }$

Vậy:

$\text{dF}=\frac{{\mu }_0\text{.}{I}_1{I}_2}{\mathrm{4\pi }\text{.}x}\text{.}{\text{dl}}_2\text{.}\text{sin}\alpha \text{.}\mathrm{d\alpha }$ (4.12)

Lực tác dụng lên đoạn dl2 ở vị trí x trên do dòng I1 chạy trong l1 gây ra là :

${\text{dF}}_x=-\frac{\mu {}_0\text{.}{I}_1\text{.}{I}_2}{\mathrm{4\pi }\text{.}x}\underset{{\alpha }_1}{\overset{{\alpha }_2}{\int }}\text{sin}\alpha \text{.}\mathrm{d\alpha }$ (4-13)

Lực tác dụng lên một đơn vị dài của dây l2 tại vị trí xi do $\overrightarrow{I_1}\text{trong}{l}_1$ gây lên là :

$F_{x_i}=\frac{{\text{dF}}_{x_i}}{{\text{dl}}_2}=\frac{{\mu }_0\text{.}{I}_1\text{.}{I}_2}{\mathrm{4\pi }}\text{.}\frac{\text{cos}{\alpha }_{\mathrm{2i}}-\text{cos}{\alpha }_{\mathrm{1i}}}{x_i}$ (4-14)

Chú ý : khi chọn các điểm tính x dọc chiều dài l2 góc  và độ dài x biến thiên dẫn đến các lực Fx biến

thiên không đều dọc chiều dài l2 của dây 2.

Điểm tác dụng của lực tổng F sẽ qua trọng tâm dây l2.

Bằng phương pháp vẽ ta có thể biết sự phân bố của lực dọc chiều dài dây l2.

1. Lực điện động giữa hai dây dẫn đặt song song trong đó một dây dài vô tận

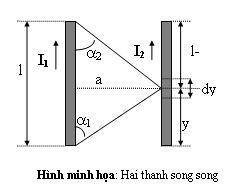
Hình minh họa, xét khi dây l1 = ; dây l2 = l khoảng cách giữa hai dây x = a. Áp dụng biểu thức (4.14) ta thay 1 = ; 2 = 0; x = a vào ta có : $F_{\text{xi}}=\frac{{\mathrm{2\mu }}_0\text{.}{I}_1\text{.}{I}_2}{\mathrm{4\pi }\text{.}a}=\text{const}$

Lực điện động tác dụng lên dây dẫn l2 là :

$F_2=\frac{{\mathrm{2\mu }}_0\text{.}{I}_1\text{.}{I}_2}{\mathrm{4\pi }}\text{.}\frac{l}{a}$ (4-14)

và có $F_2=\mathrm{0,2}\text{.}{I}_1\text{.}{I}_2\text{.}\frac{l}{a}\text{.}{\text{10}}^{-8}[\text{J/cm}]{\text{hay F}}_2=\mathrm{2,}\text{04}\text{.}{I}_1\text{.}{I}_2\text{.}\frac{l}{a}\text{.}{\text{10}}^{-8}[\text{kg}]$.

c) Lực điện động giữa hai dây dẫn song song có chiều dài bằng nhau

Áp dụng công thức (4.12) ở phần trước và thay x = a; dl2 = dy ta có :

$\text{dF}=\frac{{\mu }_0\text{.}{I}_1\text{.}{I}_2}{\mathrm{4\pi }\text{.}a}\text{.}\text{dy}(\text{cos}{\alpha }_2-\text{cos}{\alpha }_1)$ (4-15)

Trên hình 4-7 có : $\text{cos}{\alpha }_2=\frac{l-y}{(l-y{)}^2+a^2}\text{,coìn}\text{cos}{\alpha }_1=-\text{cos}(\pi -{\alpha }_1)=\frac{y}{\sqrt{y^2+a^2}}$

Vậy : $F=\frac{{\mu }_0\text{.}{I}_1\text{.}{I}_2}{\mathrm{4\pi }\text{.}a}\left[\underset{0}{\overset{l}{\int }}\frac{(l-y)\text{dy}}{\sqrt{(l-y{)}^2+a^2}}+\underset{0}{\overset{l}{\int }}\frac{\text{ydy}}{\sqrt{y^2+a^2}}\right]$ (4-16)

Tính từng tích phân riêng rẽ có :

$A=\underset{0}{\overset{l}{\int }}\frac{\text{ydy}}{\sqrt{y^2+a^2}}$

Nếu đặt z2= y2+a2 $\Rightarrow$2zdz = 2ydy và:

+ khi y= 0 thì z= a

+khi y=1 thì z= $\sqrt{l^2+a^2}$$$$$

đổi cận ta có :

$A=\underset{0}{\overset{l}{\int }}\frac{\text{ydy}}{\sqrt{y^2+a^2}}=\underset{a}{\overset{\sqrt{l^2+a^2}}{\int }}\text{dz}=\sqrt{a^2+l^2}-a\text{.}$

$\underset{0}{\overset{l}{\int }}\frac{(l-y)\text{dy}}{\sqrt{(l-y{)}^2+a^2}}=-\underset{l}{\overset{0}{\int }}\frac{\text{udu}}{\sqrt{u^2+a^2}}=\sqrt{l^2+a^2}-a$

Đổ̉i cận ta có:

$F=\frac{{\mu }_0\text{.}{I}_1\text{.}{I}_2}{\mathrm{4\pi }\text{.}a}\text{.}2\sqrt{a^2+l^2}-a=\frac{{\mu }_0\text{.}{I}_1\text{.}{I}_2}{\mathrm{2\pi }}\text{.}\frac{l}{a^2}\left[\sqrt{1+\frac{a^2}{l^2}}-\frac{a}{l}\right]$

Từ đó thay vào (4.16) ta có : $\varphi (\frac{a}{l})=\sqrt{1+\frac{a^2}{l^2}}-\frac{a}{l}\text{hay coìn goüi haìm hiãûu chènh khi l}\text{>>}\text{a thç}\varphi (\frac{a}{l})\approx 1\text{coï :}$

đặt $F=\mathrm{0,2}{I}_1\text{.}{I}_2\text{.}\frac{l}{a}\text{.}\varphi (\frac{a}{l})\text{.}{\text{10}}^{-8}[J/\text{cm}]\text{hay:}F=\mathrm{2,}\text{04}\text{.}{I}_1\text{.}{I}_2\text{.}\frac{l}{a}\text{.}\varphi (\frac{a}{l})\text{.}{\text{10}}^{-8}[\text{kg}]$

$F=\mathrm{0,2}{I}_1{I}_{2}l\text{.}\frac{1}{h^2}\left[\frac{\mathrm{2h}}{a}\text{arctg}\frac{h}{a}-\text{ln}l+\frac{h^2}{a^2}\right]\text{.}{\text{10}}^{-8}[J/\text{cm}]$

Khi hai thanh dẫn có tiết diện chữ nhật với kích thước rộng b, cao h và dài l

+ Nếu có b  h, b  a thì :

$F=\mathrm{0,2}\text{.}{I}_1{I}_2\frac{l}{a}\text{.}{\text{10}}^{-8}\varphi (f)[J/\text{cm}]$. Có thể viết dưới dạng :

$F=\mathrm{2,}\text{04}\text{.}{I}_1{I}_2\frac{l}{a}\text{.}{\text{10}}^{-8}\varphi (f)[\text{kg}]$hay $j$

có $\frac{h}{a};\frac{a-b}{h+b}$ (f) gọi là hàm Dwight phụ thuộc theo $$$F=\mathrm{2,}\text{04}\text{.}{I}_1{I}_2\frac{l}{a}\text{.}{\text{10}}^{-8}\varphi (f)[\text{kg}]$

+ Nếu h<<a ; h/b<1 thì:

$\varphi (f)=\frac{a^2}{b^2}[(1+\frac{a}{b})+(1-\frac{b}{a})\text{.}\text{ln}(1-\frac{b}{a})]$

Trong đó : $\sqrt{2}$.

Mạch xoay chiều một pha

Xét hai dây dẫn song song có hai dòng điện i1, i2 cùng pha (hoặc lệch một góc ) giả thiết i1 = i2 = Imsint = I $F=C\text{.}{I}_m^2\text{.}{\text{sin}}^2\omega \text{.}t=C\text{.}{I}_m^2\text{.}\frac{1-\text{cos}\mathrm{2\omega }\text{.}t}{2}=\frac{C\text{.}{I}_m^2}{2}-\frac{C\text{.}{I}_m^2\text{.}\text{cos}\mathrm{2\omega }\text{.}t}{2}=F_1+F_2$sint = i

Lực điện động F = C.i2 , với C là hằng số :

Hình 4-8: Lực điện động trong mạch một pha $F_1=\frac{{\text{CI}}_m^2}{2}$

Trong đó :

$F_2=-\frac{{\text{CI}}_m^2\text{.}\text{cos}\mathrm{2\omega t}}{2}=-F_1\text{cos}\mathrm{2\omega t}$là thành phần không đổi.

$F_{\text{tb}}=\frac{C\text{.}{I}_m^2}{2}={\text{CI}}^2$là

thành phần lực thay đổi.

Ta biểu diễn như hình 4-8 :

Lực F biến thiên khoảng từ 0 đến CIm2.

- Lực trung bình $i=\sqrt{2}\text{.}Ie^{-\frac{t}{T}}-\text{cos}\mathrm{\omega t}$

Khi xảy ra ngắn mạch lực F rất lớn, dòng điện $\lambda =\frac{1}{T}$

Hình 4-9: Lực điện động khi ngắn mạchĐặt $\lambda =\text{22}$ là hệ số cản của dòng không tuần hoàn, phụ thuộc vào máy phát điện và các thông số của mạch điện. Theo thí nghiệm có $F={\text{Ci}}^2=2{\text{CI}}^2(e^{-\mathrm{\lambda t}}-\text{cos}\mathrm{\omega t}{)}^2$, ta có lực điện động là:

$\sqrt{2}$

Tức là trong mạch gồm hai thành phần là thành phần biến đổi tuần hoàn và thành phần không tuần hoàn. Sau một số chu kì (nT) thành phần không tuần hoàn suy giảm về 0, do đó lực ổn định (một số nửa chu kì đỉnh nhọn thấp dần, một số nửa cao dần đến bằng nhau và ổn định như hình 4-9).

Theo thí nghiệm sau t =  thì có i đạt cực đại imax = 1,8 $\begin{array}{}{i}_1=I\sqrt{2}\text{.}\text{sin}\omega \text{.}t\\ i_2=I\sqrt{2}\text{.}\text{sin}(\omega \text{.}t-\frac{\mathrm{2\pi }}{3})\\ i_2=I\sqrt{2}\text{.}\text{sin}(\omega \text{.}t+\frac{\mathrm{2\pi }}{3})\\ \\ \\ \\ \begin{array}{}\{\{\end{array}\\ \end{array}$I và lực:

FMax = CI2 = C.6,48I2.

Lực điện động trong mạch xoay chiều ba pha

Fđ1 Fk1 AFđ2 Fk2 BCa)YXABCFACFAB

b)Hình 4-10: Lực điện động trong mạch xoay chiều ba pha Giả sử dòng điện trong các pha A, B, C lần lượt là :

$\begin{array}{}F=C_1{i}_1{i}_2+C_3{i}_1{i}_3\\ ={\mathrm{2I}}^2\left[C_1\text{sin}\mathrm{\omega t}\text{.}\text{sin}(\mathrm{\omega t}-\frac{\mathrm{2\pi }}{3})+C_3\text{sin}\mathrm{\omega t}\text{.}\text{sin}(\mathrm{\omega t}+\frac{\mathrm{2\pi }}{3})\right]\end{array}$

a) Khi bố trí ba dây trên một mặt phẳng (hình 4-10a)

Gọi C1 hằng số lực giữa dây A và B, C2 dây B và C, C3 dây A và C . Ta có:

+ Lực tác dụng lên dây pha A là:

$F_{k_1}=\frac{I^2}{2}\left[2\sqrt{C_1^2+C_3^2-C_1{C}_3}-(C_1+C_3)\right]$

Chọn chiều tăng theo thời gian t: dấu (+) với lực kéo về hai dây kia và (-) với lực đẩy ra. Tiến hành thay số ta tính toán và tìm được các trị số lực đẩy và lực kéo cực đại của pha A là: $F_{{â}_1}=-\frac{I^2}{2}\left[2\sqrt{C_1^2+C_3^2-C_1{C}_3}+(C_1+C_3)\right]$.

Chọn sin2t và cos2t dấu (-) lực ngược lại là lực đẩy nhau:

$F_{k_2}=\frac{I^2}{2}\left[2\sqrt{C_1^2+C_2^2+C_1{C}_2}-(C_1-C_2)\right]$.

+ Với dây pha C giống dây A.

+ Dây pha B : tương tự ta có Fk2 và Fđ2 là :

$F_{{â}_2}=-\frac{I^2}{2}\left[2\sqrt{C_1^2+C_2^2+C_1{C}_2}-(C_1-C_2)\right]$.

$\begin{array}{}{F}_{k_1}=\mathrm{0,}\text{115}\text{.}{C}_1{I}^2\\ F_{{â}_1}=-\mathrm{1,}\text{615}\text{.}{C}_1{I}^2\\ \\ \\ \\ \begin{array}{}\{\end{array}\\ \end{array}$.

Nếu chọn C1 = C2, C3 = 0,5C1 thì ta có pha A: $\begin{array}{}{F}_{k_2}=\mathrm{1,}\text{73}{C}_1{I}^2\\ F_{{â}_2}=-\mathrm{1,}\text{73}{C}_1{I}^2\\ \\ \\ \\ \begin{array}{}\{\end{array}\\ \end{array}$

Có nghĩa là ở pha A lực đẩy gấp khoảng 14 lần lực kéo. Còn ở pha B thì:

$F=\frac{\sqrt{3}}{2}{\text{CI}}^2\sqrt{2-2\text{.}\text{cos}\mathrm{2\omega t}}=\sqrt{3}{I}^{2}C\text{.}\text{sin}\mathrm{\omega t}$

b) Trường hợp ba dây dẫn bố trí trên ba đỉnh tam giác đều

Ta giả thiết lần lượt ba dòng điện i1, i2, i3 cho ở trên đi vào dây dẫn các pha A, B, C được bố trí trên ba đỉnh tam giác đều như hình 4-10b.

Ta có hệ số C1=C2=C3=C

+ Lực tác dụng lên dây pha A sau khi thay số và tính toán ta được:

$\begin{array}{}{i}_1=\sqrt{2}I\left[e^{-\mathrm{\lambda t}}\text{cos}\varphi -\text{cos}(\mathrm{\omega t}+\varphi )\right]\\ i_2=\sqrt{2}I\left[e^{-\mathrm{\lambda t}}\text{cos}(\varphi -\frac{\mathrm{2\pi }}{3})-\text{cos}(\mathrm{\omega t}+\varphi -\frac{\mathrm{2\pi }}{3})\right]\\ i_3=\sqrt{2}I\left[e^{-\mathrm{\lambda t}}\text{cos}(\varphi +\frac{\mathrm{2\pi }}{3})-\text{cos}(\mathrm{\omega t}+\varphi +\frac{\mathrm{2\pi }}{3})\right]\\ \\ \\ \\ \begin{array}{}\{\{\end{array}\\ \end{array}$

+ Lực tác dụng lên dây B và dây C tương tự như dây A chỉ có góc pha thay đổi.

Lực điện động trong ba pha khi ngắn mạch

Dòng trong các pha khi ngắn mạch là :

$F_{{â}_1}=-\sqrt{3}{C}_1{\mathrm{2I}}^2{\text{sin}}^2\frac{\mathrm{\omega t}}{2}\left[\frac{\sqrt{3}}{2}-\text{cos}\mathrm{\omega t}\right]$

Trong đó :

 :góc pha của dòng điện trong pha thứ nhất khi bắt đầu xảy ra sự cố;  : hệ số cản. Nếu giả thiết không xét đến thành phần không tuần hoàn với e-t = 1 ta có :

+ Lực tác động dây A là : F = C1i1i2 + C3i1i3

+ Lực tác dụng lên dây B là : F = C1i1i2 + C2i2i3

Khi xét ba dây cùng nằm trong một mặt phẳng, lực điện động không chỉ phụ thuộc thời gian t mà phụ thuộc cả thời điểm xảy ra ngắn mạch .

Xét : +) Khi  = - 150 mà xảy ra ngắn mạch thì $\begin{array}{}{F}_{{â}_{1\text{max}}}=-\mathrm{6,}\text{46}{C}_1{I}^2\\ F_{k_1}=0\\ \\ \\ \\ \begin{array}{}\{\end{array}\\ \end{array}$

Nếu t =  thì $F_{k_1}=-\sqrt{3}{C}_1{\mathrm{2I}}^2{\text{sin}}^2\frac{\mathrm{\omega t}}{2}\left[\frac{\sqrt{3}}{2}+\text{cos}\mathrm{\omega t}\right]$

+) Khi  = 750 mà ngắn mạch thì $Z=\frac{\text{112}}{l^2}\sqrt{\frac{E\text{.}J}{g_1}}$

t =  thì Fk1max = 0,16C1I2, Fđ1max = -1,5C1I2.

Cộng hưởng cơ khí

Khi dòng điện xoay chiều đi qua thanh dẫn (thanh cái) lực điện động sẽ gây chấn động và có thể phát sinh hiện tượng cộng hưởng cơ khí.

Điều kiện tránh cộng hưởng cơ khí

Muốn không xảy ra cộng hưởng thì tần số dao động riêng của thanh cái phải bé hơn tần số sóng cơ bản của lực. Trong thực tế người ta thường thay đổi khoảng cách giá đỡ thanh cái để điều chỉnh trị số tần số dao động riêng của thanh cái.

Tần số dao động riêng thanh cái tính theo biểu thức :

$\sqrt{2}{I}_{\text{âm}}{K}_m\ge i_{\text{xk}}$

Trong đó :

l : khoảng cách giá đỡ cách điện; E : mô đun đàn hồi [kg/cm2].

J : mô men quán tính (lấy trục thẳng góc với hướng uốn làm chuẩn)

g1 : trọng lượng đơn vị dài thanh cái [kg].

Nếu không thực hiện được điều kiện trên thì có thể phải giải quyết bằng điều chỉnh tần số riêng của thanh cái z để lớn hơn tần số sóng cơ bản. Chú ý tần số lực điện động gấp hai lần tần số dòng điện f1 = 2fI’ > z.

Ổn định lực điện động

Trong thiết bị điện phải tính lực điện động để kiểm tra xem thiết bị điện có đạt độ bền cơ hay không. Ổn định lực điện động là khả năng chịu đựng tác động cơ khí do lực điện động sinh ra khi ngắn mạch.

Để đảm bảo cần điều kiện cần thì: Im > Ixk với :

+Im : dòng cho phép lớn nhất của thiết bị điện, ixk : dòng xung kích tính toán khi ngắn mạch ba pha. Có thể dùng bội số cho phép (Km) lớn nhất để kiểm tra lực điện động.

$I_m=i_{\text{xk}}\approx \mathrm{2,}\text{55}\frac{S_{\text{ng}}}{\sqrt{3}{U}_{\text{âm}}}[\text{kA}]$, trong đó : Km là bội số dòng cho phép lớn nhất.

Chú ý : theo tính toán ngắn mạch trong mạng ba pha, lực điện động khi ngắn mạch một pha (Fmax = CI12 = C.6,48Iđm2) lớn hơn lực điện động khi ngắn mạch ba pha (Fđ1max = C1.6,46Iđm2), nhưng do khi ngắn mạch ba pha chiều lực thay đổi trong không gian nên phải dùng để kiểm tra khả năng chịu lực ở các điểm.

- Nếu thiết bị điện không ghi giá trị Im thì có thể xác định theo công thức :

Với : Sng : công suất ngắt mạch [MVA]; Uđm : điện áp định mức hiệu dụng [kV].