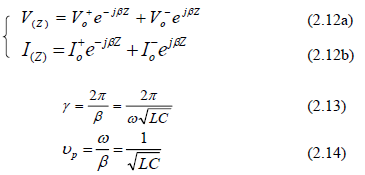Mô hình
- Vì các đường truyền cho sóng TEM luôn có ít nhất hai vật dẫn nên thông thường chúng được mô tả bởi hai dây song hành, trên đó mỗi đoạn có chiều dài ∆ z có thể được coi như là một mạch có phần tử tập trung với R, L, G, C là các đại lượng tính trên một đơn vị chiều dài.
R: Điện trở nối tiếp trên một đơn vị chiều dài cho cả hai vật dẫn, Ω/m
L: Điện cảm nối tiếp trên một đơn vị đo chiều dài cho cả hai vật dẫn, H/m
G: Dẫn nạp shunt trên đơn vị chiều dài, S/m. C: Điện dung shunt trên đơn vị chiều dài, F/m
* L biểu thị độ tự cảm tổng của hai vật dẫn và C là điện dung do vị trí tương đối gần nhau của hai vật dẫn. R xuất hiện do độ dẫn điện hữu hạn của các vật dẫn và G mô tả tổn hao điện môi trong vật liệu phân cách các vật dẫn. Một đoạn dây hữu hạn có thể coi như một chuỗi các khâu như (hình 2.1)
- Áp dụng định luật Kirchhoff cho hình 2.1 =>
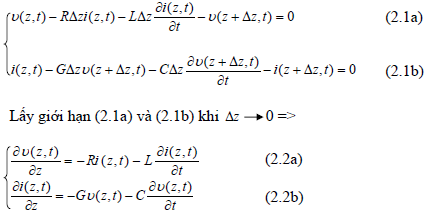
Đây là các phương trình dạng time – domain của đường dây (trong miền thời gian), còn có tên là các phương trình telegraph.
Nếu v (z, t) và i (z, t) là các dao động điều hòa ở dạng phức thì (1.2) →
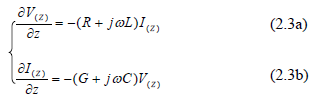
(2.3) Có dạng tương tự hai phương trình đầu của hệ phương trình Maxwell
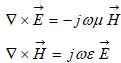
Sự truyền sóng trên đường dây
Dễ thấy có thể đưa (2.3 a,b) về dạng
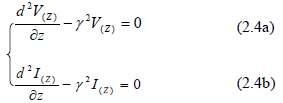
Trong đó là hằng số truyền sóng phức, là một hàm của tần số. Lời giải dạng sóng chạy của (2.4) có thể tìm dưới dạng :
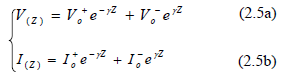
Từ 2.5b có thể viết dưới dạng :
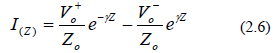
Chuyển về miền thời gian thì sóng điện áp có thể được biểu diễn bởi :
![]()
Trong đó: là góc pha của điện áp phức
Khi đó bước sóng được tính bởi: (2.8)
Vận tốc pha: (2.9)
Đường dây không tổn hao
(2.7) là nghiệm tổng quát cho đường dây có tổn hao với hằng số truyền và trở kháng đặc trưng có dạng phức. Trong nhiều trường hợp thực tế tổn hao đường dây rất bé, có thể bỏ qua khi đó có thể coi R = G = 0 và ta có
![]()
» Trở kháng đặc trưng: là một số thực
Khi đó: