Trong các chương trước ta đã xét một vài chương trình đơn giản. Thấy rằng những chương trình này thực sự rất đơn giản, chỉ gồm một vài lệnh thực hiện tuần tự là dẫn đến kết quả bài toán cần giải. Trong chương này, sẽ giới thiệu những lệnh của Fortran cho phép ta điều khiển được thứ tự các bước cần thực hiện. Sự điều khiển được thực hiện thông qua những lệnh cho phép ta chọn những nhánh khác nhau trong chương trình và những lệnh cho phép ta lặp lại những phần nào đó của chương trình. Những lệnh như vậy gọi là những lệnh điều khiển.
Khái niệm về cấu trúc thuật toán
Các thao tác cơ bản. Giả trình và lưu đồ
Trong mục 1.3, chương 1 đã sơ lược nói về quy trình năm bước giải bài toán. Đối với những bài toán phức tạp về cách giải thì bước 4 là bước khó khăn nhất. Người lập trình phải mô tả tuần tự các công đoạn từ đầu đến cuối quá trình giải, chia quá trình này thành một số khối và liệt kê những khối đó ra để sau này chương trình máy tính sẽ tuần tự thực hiện. Trong mỗi khối người lập trình lại phải chi tiết hóa thêm đến mức có thể chuyển thành những lệnh máy tính. Cách chia khối và chi tiết hóa từng khối như vậy có thể gọi là phương pháp chia và chinh phục. Kết quả cuối cùng của chia khối và chi tiết hóa từng khối chính là thuật giải (algorithm).
Bảng 4.1. Các thao tác cơ bản và quy ước tương ứng trong giả trình và lưu đồ

Những hình thức để biểu diễn trực quan thuật giải sao cho dễ dàng chuyển thành chương trình là giả trình và lưu đồ. Một người lập trình có thể chọn hình thức này hoặc hình thức kia. Theo cách giả trình, mỗi cấu trúc của thuật giải được quy ước bởi một chú giải ngắn gọn gần giống với ngôn ngữ viết của chúng ta; còn trong cách biểu diễn lưu đồ, mỗi cấu trúc đó được mô tả bằng một biểu tượng hình học.
Dần dần ta sẽ thấy rằng, nói chung những thao tác cơ bản trong một thuật giải thường là những tính toán, nhập, xuất dữ liệu và so sánh. Nói chung một chương trình máy tính dù đơn giản hay phức tạp đến đâu cũng chỉ gồm có những thao tác cơ bản đó. Một số thao tác (hay lệnh) có thể nhóm lại với nhau tạo thành một khối hay một khối cấu trúc. Những chú giải giả trình và những biểu tượng lưu đồ chính là để thể hiện những thao tác cơ bản đó (xem bảng 4.1).
Các cấu trúc tổng quát trong thuật giải
Các bước trong một thuật giải có thể phân chia thành ba dạng cấu trúc tổng quát - đó là cấu trúc tuần tự, lựa chọn và lặp. Cấu trúc tuần tự là chuỗi các bước thực hiện một cách kế tiếp nhau. Cấu trúc lựa chọn (hay còn gọi là cấu trúc rẽ nhánh) cho phép so sánh hai giá trị, sau đó tùy kết quả so sánh mà định ra một chuỗi các bước khác nhau phải thực hiện. Cấu trúc lặp được dùng khi quá trình giải cần lặp lại một số thao tác cho đến khi thỏa mãn một điều kiện. Trong thuật giải phức tạp hơn một chút có thể thấy các cấu trúc tổng quát này lồng vào nhau, trong cấu trúc lặp có những đoạn gồm những thao tác tuần tự được thực hiện, có những đoạn xuất hiện sự rẽ nhánh tùy theo một điều kiện so sánh nào đó.
Thí dụ ứng dụng thuật toán cấu trúc
Bây giờ ta tìm hiểu phương pháp xây dựng thuật giải theo kỹ thuật chia khối và chi tiết hóa từng khối, phân tích cấu trúc thuật giải thông qua một thí dụ cụ thể về bài toán phân tích các số liệu thực nghiệm.
1) Phát biểu bài toán: Xác định giá trị lớn nhất, nhỏ nhất và biên độ các giá trị của tập số liệu quan trắc.
2) Mô tả dữ liệu vào và ra: Dữ liệu vào là một chuỗi các số liệu quan trắc. Đầu ra là trị cực đại, cực tiểu và biên độ các giá trị.
3) Tính thử với tập số liệu quan trắc sau:
Chuỗi số liệu thử:
40.56
55.92
66.31
58.35
62.88
41.99
49.70
53.21
Thực hiện tìm trị cực đại như sau: Trước hết so sánh số thứ nhất của chuỗi với số thứ hai để xác định số lớn hơn, coi là cực đại tạm thời. Bây giờ xét số thứ ba và so sánh nó với cực đại tạm thời. Nếu cực đại tạm thời lớn hơn, ta xét tới số thứ tư; nhưng nếu số thứ ba lớn hơn cực đại tạm thời, ta thay thế số đó vào cực đại tạm thời. Tiếp tục quá trình này với toàn bộ chuỗi số liệu sẽ dẫn tới kết quả là cực đại tạm thời chính là trị cực đại trong cả chuỗi. Một quá trình tương tự sẽ cho phép tìm cực tiểu. Với tập số liệu đang xét, kết quả là:
Giá trị cực đại = 66.31
Giá trị cực tiểu = 40.56
Tính biên độ bằng hiệu giữa cực đại và cực tiểu = 66.31 - 40.56 = 25.73
4) Xây dựng thuật giải: Khái quát lại các bước thực hiện ở bước (3) ta có thể chia bài toán thành ba khối:
- Đọc số liệu và xác định các trị cực đại và cực tiểu
- Tính hiệu giữa cực đại và cực tiểu để nhận biên độ
- In cực đại, cực tiểu và biên độ
Với thí dụ này, ta chi tiết hóa cách giải bằng giả trình. Rõ ràng khối thứ nhất đòi hỏi phải chi tiết hóa nhiều hơn nữa, vì nó vừa bao gồm cả việc chọn trị cực đại, cực tiểu xuất phát, vừa bao gồm cả quá trình lặp (lặp để đọc số liệu và lặp để cập nhật cực trị khi cần). Cực đại và cực tiểu xuất phát thường được gán bằng giá trị của quan trắc thứ nhất, do đó ta đọc một số liệu đầu để gán cho chúng. Sau đó ta đọc số thứ hai và đi vào vòng lặp. "Chừng nào số không phải là zero", ta cập nhật trị cực đại và cực tiểu nếu cần thiết. Bây giờ ta mô tả những bước đã đủ chi tiết này bằng giả trình như sau:
Giả trình: Đọc số
Cực đại Số
Cực tiểu Số
Đọc số
Chừng nào số không bằng zero thì
Nếu số > Cực đại thì
Cực đại Số
Nếu số < Cực tiểu thì
Cực tiểu Số
Đọc số
Biên độ Cực đại - Cực tiểu
In 'GIA TRI CUC DAI = ', Cực đại
In 'GIA TRI CUC TIEU = ', Cực tiểu
In 'BIEN DO GIA TRI = ', Biên độ
Đây là một thuật giải đơn giản. Chỉ có một khối thứ nhất cần chi tiết hóa. Thấy rằng khi thuật giải đã chi tiết hóa tới mức như vậy, thì việc chuyển thành chương trình Fortran sẽ không còn là vấn đề khó khăn. Trong các mục tiếp sau, ta sẽ nghiên cứu các lệnh Fortran chuyên trợ giúp cho việc thiết kế các cấu trúc điều khiển của bài toán này và nhiều bài toán tương tự.
Cấu trúc IF và các lệnh tương ứng
Biểu thức lôgic
Biểu thức lôgic được tạo bởi các toán tử quan hệ:
.EQ. bằng .NE. không bằng
.LT. nhỏ hơn .LE. nhỏ hơn hoặc bằng
.GT. lớn hơn .GE. lớn hơn hoặc bằng
nối hai biến số ở hai bên.
Tùy theo quan hệ giữa hai biến số đó mà biểu thức lôgic có một trong hai giá trị lôgic:
đúng (.TRUE.) hoặc sai (.FALSE.).
Thí dụ, xét biểu thức A .EQ. B trong đó A và B là các biến số thực. Nếu giá trị của A bằng giá trị của B thì biểu thức lôgic sẽ có giá trị là đúng .TRUE.. Nếu không thì biểu thức có giá trị là sai .FALSE.. Tương tự, nếu X bằng 4,5 thì biểu thức X .GT. 3.0 có giá trị bằng đúng .TRUE..
Ta có thể nối hai biểu thức lôgic bằng một trong các toán tử lôgic.OR. và .AND. thành một biểu thức lôgic kết hợp.
Khi hai biểu thức lôgic nối với nhau bởi .OR. thì biểu thức lôgic kết hợp sẽ có giá trị là đúng nếu một hoặc cả hai biểu thức có giá trị là đúng. Ta có thể gọi .OR. là toán tử cộng lôgic.
Khi hai biểu thức nối với nhau bởi .AND. thì biểu thức kết hợp có giá trị đúng chỉ khi cả hai biểu thức có giá trị là đúng. Ta có thể gọi toán tử .AND. là toán tử nhân lôgic.
Toán tử .NOT. có thể đứng trước biểu thức lôgic và đổi giá trị của nó thành giá trị ngược lại. Thí dụ, nếu A. GT. B là đúng (giá trị bằng .TRUE.) thì .NOT. A. GT. B là sai (.FALSE.).
Một biểu thức lôgic có thể chứa nhiều toán tử lôgic, thí dụ như trong biểu thức sau:
.NOT. (A .LT. 15.4) .OR. KT .EQ. ISUM
Quyền ưu tiên từ cao nhất xuống thấp nhất là
.NOT., .AND. và .OR.
Trong biểu thức trên, biểu thức A .LT. 15.4 sẽ được ước lượng trước tiên, sau đó giá trị của nó (.TRUE. hoặc .FALSE.) được đổi ngược lại. Giá trị này sẽ được xét cùng với giá trị của KT .EQ. ISUM. Thí dụ, nếu A là 5.0, KT là 5 và ISUM là 5, thì biểu thức bên trái của toán tử .OR. có giá trị sai .FALSE., biểu thức bên phải có giá trị đúng .TRUE. và toàn bộ biểu thức sẽ có giá trị là đúng .TRUE..
Giá trị của biểu thức lôgic có thể được gán cho biến lôgic bằng lệnh gán giống như lệnh gán dùng với các biến số và biểu thức số, thí dụ:
LOGICAL DONE, OK
DONE = .FALSE.
OK = DONE .AND. I .GT. 24
Khi so sánh hai biểu thức lôgic hay hai biến lôgic có tương đương nhau hay không, trong Fortran không dùng các toán tử quan hệ như khi so sánh hai biểu thức số, mà dùng các toán tử lôgic .EQV. và .NEQV..
Bảng 4.2. tóm tắt quy tắc ước lượng của các toán tử lôgic cho mọi trường hợp có thể xảy ra.
Bảng 4.2. Các toán tử lôgic
| A | B | .NOT. A | A.AND.B | A.OR.B | A.EQV.B | A.NEQV.B |
| False | False | True | False | False | True | False |
| False | True | True | False | True | False | True |
| True | False | False | False | True | False | True |
| True | True | False | True | True | True | False |
Khi các toán tử số học, quan hệ và lôgic cùng có mặt trong một biểu thức thì các toán tử số học thực hiện trước tiên; sau đó các toán tử quan hệ dùng để phát sinh các giá trị TRUE hoặc FALSE; và các giá trị này được đánh giá bằng các toán tử lôgic theo thứ tự ưu tiên .NOT., .AND., và .OR.. Các quan hệ .EQV. và .NEQV. được thực hiện sau cùng.
Lệnh IF lôgic
1) Các lệnh IF lôgic có thể có một số dạng sử dụng. Dạng thứ nhất gọi là Logical IF viết như sau:
IF (Biểu thức lôgic) Lệnh thực hiện
Theo lệnh này, nếu biểu thức lôgic ở trong cặp dấu ngoặc đơn có giá trị True thì thực hiện lệnh nằm trên cùng dòng với biểu thức lôgic, nếu biểu thức lôgic có giá trị False thì không thực hiện lệnh cùng dòng mà chuyển ngay tới lệnh tiếp theo phía dưới trong chương trình. Chú ý rằng lệnh thực hiện ghi sau biểu thức lôgic có thể là một trong những lệnh tính toán (gán), xuất, nhập dữ liệu..., nhưng không thể là một lệnh IF khác. Biểu thức lôgic bao giờ cũng phải đặt trong cặp dấu ngoặc đơn. Thí dụ, những lệnh IF sau đây là những lệnh đúng:
IF (A. GT. 0.0) SUM = SUM + A
IF (TIME .GT. 1.5) READ *, DIST
2) Dạng thứ hai gọi là Block IF: Nếu biểu thức lôgic có giá trị True máy thực hiện các lệnh từ lệnh 1 đến lệnh , sau đó chuyển tới lệnh tiếp sau END IF. Nếu biểu thức lôgic có giá trị False, điều khiển chuyển ngay xuống lệnh đứng sau END IF:
3) Dạng thứ ba gọi là dạng IF - ELSE: Khi biểu thức lôgic có giá trị True các lệnh từ 1 đến được thực hiện, nếu biểu thức lôgic có giá trị False các lệnh từ đến được thực hiện:
4) Dạng thứ tư gọi là IF - ELSE IF: Nếu biểu thức lôgic 1 có giá trị True thì loạt các lệnh từ 1 đến được thực hiện; nếu biểu thức lôgic 1 có trị False, biểu thức lôgic 2 có trị True thì loạt lệnh từ đến thực hiện; nếu các biểu thức lôgic 1 và 2 là False và biểu thức lôgic 3 True thì các lệnh từ tới thực hiện. Nếu không một biểu thức lôgic nào có giá trị True thì chỉ có các lệnh từ tới được thực hiện. Trong thực tế ta có thể cấu tạo số nhánh ELSE IF nhiều hơn hoặc ít hơn, chứ không nhất thiết chỉ là hai nhánh như đã viết dưới đây:

Thí dụ 1:Sử dụng các lệnh IF lôgic để điều khiển rẽ nhánh. Lập chương trình giải hệ phương trình bậc hai
(các hệ số nhập từ bàn phím, ).
Ta có thể cụ thể hóa thuật giải của bài toán này bằng lưu đồ như trên hình 4.1. Từ đó viết mã nguồn của chương trình Fortran như dưới đây.

PRINT * , ' HE SO A BANG'
READ * , A
PRINT * , ' HE SO B BANG'
READ * , B
PRINT * , ' HE SO C BANG'
READ * , C
DELT = B**2 - 4.*A*C
IF (DELT .LT. 0.) THEN
PRINT * , ' PHUONG TRINH VO NGHIEM'
ELSE IF (DELT .EQ. 0.) THEN
PRINT 5 , -B / (2.0 *A)
5 FORMAT (1X, 'NGHIEM KEP BANG' , F10.2)
ELSE
DELT = SQRT (DELT)
A = 2. * A
PRINT 7 , (-B + DELT) / A , (-B - DELT) / A
7 FORMAT (1X, 'HAI NGHIEM: X1 = ',
* F10.2, 5X, 'X2 = ', F10.2)
END IF
END
Lệnh IF số học
Lệnh IFsố học cho phép thực hiện rẽ nhánh chương trình thành ba nhánh tùy thuộc vào giá trị của biểu thức số học, dạng tổng quát của lệnh này viết như sau:
IF ( Biểu thức số học )
trong đó nhãn của các lệnh thực hiện. Nếu biểu thức số học có giá trị âm thì điều khiển được chuyển tới lệnh có nhãn là , bằng không - nhãn , và dương - nhãn .
Thí dụ, theo lệnh
IF (I - 10) 4, 8, 7
nếu điều khiển chuyển đến lệnh có nhãn là 4, nếu chuyển đến nhãn 8 và nếu chuyển đến nhãn 7.
Trong lệnh
IF (X - 3.5) 3, 6, 6
khi điều khiển chuyển tới lệnh có nhãn là 6, khi điều khiển chuyển tới lệnh có nhãn là 3.
Thí dụ 2: Dùng lệnh IF số học để thiết kế vòng lặp. Viết chương trình tính và in giá trị hàm
,
trong đó biến thiên từ 1 đến 3 với bước 0,1 và .
Lưu đồ giải bài toán này tham khảo trên hình 4.2.

| T = 0.1 | |
| X = 1.0 | |
| 12 | F = EXP (- X ** 3) * COS (T * X + 1) |
| WRITE (6 , 9) X , F | |
| 9 | FORMAT (F5.2, E12.2) |
| X = X + 0.1 | |
| IF (X - 3.0) 12 , 12 , 4 | |
| 4 | STOP |
| END |
Lệnh chuyển điều khiển vô điều kiện GO TO
Lệnh này có dạng
GO TO
trong đó nhãn của lệnh mà điều kiển cần chuyển tới.
Lệnh cần chuyển tới nhất thiết phải có nhãn. Ngoài ra trong chương trình không thể có những lệnh có cùng nhãn như nhau. Lệnh GO TO có thể chuyển điều khiển tới bất kỳ lệnh thực hiện nào đứng trước hoặc đứng sau lệnh GO TO. Thí dụ:
| GO TO 5 | 7 | I = I + 1 | |
| . . . | X (I)=Y (I) | ||
| 5 | X = X + 1.0 | GO TO 7 |
Thí dụ 3: Viết chương trình nhập phần tử của mảng một chiều X, sắp xếp lại các phần tử mảng đó theo thứ tự tăng dần và in ra màn hình.
| REAL X (20), TG | |
| INTEGER N, I, J, K | |
| N = 10 | |
| PRINT * , 'NHAP CAC PHAN TU MANG' | |
| I = 0 | |
| 7 | I = I + 1 |
| PRINT *, 'PHAN TU ', I | |
| READ *, X (I) | |
| IF (I .LT. N) GOTO 7 | |
| C Sắp xếp mảng X theo thứ tự tăng dần | |
| I = 1 | |
| 2 | K = I |
| J = I + 1 | |
| 1 | IF (X (J) .LT. X (K)) K = J |
| J = J + 1 | |
| IF (J .LE. N) GOTO 1 | |
| TG = X(I) | |
| X(I) = X(K) | |
| X(K) = TG | |
| I = I + 1 | |
| IF (I. LT. N) GOTO 2 | |
| C Lần lượt in các giá trị của mảng X đã sắp xếp | |
| I = 1 | |
| 3 | PRINT 8 , X(I) |
| 8 | FORMAT (F12.2) |
| I = I + 1 | |
| IF (I .LE. N) GOTO 3 | |
| END |
Lệnh GO TO tính toán
Lệnh GO TO tính toán dùng để thực hiện chuyển điều khiển tới một trong số những lệnh có nhãn được liệt kê trong lệnh GOTO tùy thuộc vào giá trị của một biến trong lệnh. Dạng tổng quát của lệnh như sau:
GO TO ( ) ,
trong đó các nhãn của những lệnh thực hiện, biến nguyên không chỉ số. Theo lệnh này, điều khiển được chuyển tới một trong các lệnh tùy thuộc vào giá trị của , cụ thể khi điều khiển sẽ chuyển tới lệnh có nhãn , khi nhãn , ..., khi nhãn . Nếu giá trị của nằm ngoài khoảng thì điều khiển chuyển xuống lệnh đứng sau lệnh GO TO để thực hiện.
Thí dụ, theo lệnh
GO TO (17 , 2 , 115 , 19) , KA
khi KA = 1 điều khiển chuyển tới lệnh có nhãn là 17, khi KA = 2 điều khiển chuyển tới lệnh có nhãn là 2, khi KA = 3 điều khiển chuyển tới lệnh có nhãn là 115 và khi KA = 4 điều khiển chuyển tới lệnh có nhãn là 19.
Thí dụ 4: Ứng dụng lệnh GOTO tính toán. Viết chương trình tính giá trị của đa thức Lejandre với theo công thức
| REAL X, P | |
| INTEGER L, I | |
| X = 0.4 | |
| L = 0 | |
| 28 | I = L + 1 |
| GO TO (12, 17, 21, 6) , I | |
| 12 | P = 1.0 |
| GO TO 24 | |
| 17 | P = X |
| GO TO 24 | |
| 21 | P = 0.5 * (3.0 * X ** 2 - 1.0) |
| GO TO 24 | |
| 6 | P = 0.5 * (5.0 * X ** 3 - 3.0 * X) |
| 24 | WRITE (* , 8) L , P |
| 8 | FORMAT (I3 , F12.5) |
| L = L + 1 | |
| IF (L - 3) 28 , 28 , 30 | |
| 30 | STOP |
| END |
Thí dụ 5: Sắp xếp danh sách. Viết chương trình nhập họ tên và điểm ba môn học của nhóm gồm sinh viên. Tính điểm trung bình cộng ba môn học. In bảng có tiêu đề và các cột thứ tự, họ tên, điểm ba môn và điểm trung bình, ghi chú xếp loại theo điểm trung bình: trung bình , khá , giỏi . Danh sách xếp theo thứ tự từ cao xuống thấp dựa theo điểm trung bình.
| PARAMETER (N = 15) | |
| INTEGER I , J , K , D1 (50) , D2 (50) , D3 (50), ID | |
| REAL D , TB (50) | |
| CHARACTER * 20 TEN (50) , TENTG | |
| C Nhập họ tên, điểm thi và tính điểm trung bình | |
| I = 0 | |
| 7 | I = I + 1 |
| PRINT * , ' NHAP SINH VIEN ' , I | |
| READ (* , '(A20)') TEN(I) | |
| READ * , D1 (I) , D2 (I) , D3 (I) | |
| TB (I) = (D1 (I) + D2 (I) + D3 (I)) / 3.0 | |
| IF (I .LT. N) GO TO 7 | |
| C Sắp xếp danh sách theo thứ tự điểm trung bình giảm dần | |
| I = 1 | |
| 2 | K = I |
| J = I + 1 | |
| 1 | IF (TB(J) .GT. TB(K)) K = J |
| J = J + 1 | |
| IF (J .LE. N) GO TO 1 | |
| TENTG = TEN (I) | |
| TEN (I) = TEN (K) | |
| TEN (K) = TENTG | |
| ID = D1 (I) | |
| D1 (I) = D1 (K) | |
| D1 (K) = ID | |
| ID = D2 (I) | |
| D2 (I) = D2 (K) | |
| D2 (K) = ID | |
| ID = D3 (I) | |
| D3 (I) = D3 (K) | |
| D3 (K) = ID | |
| D = TB (I) | |
| TB (I) = TB (K) | |
| TB (K) = D | |
| I = I + 1 | |
| IF (I .LT. N) GO TO 2 | |
| C In tiêu đề danh sách lên màn hình | |
| PRINT 100 | |
| 100 | FORMAT (21X , 'BANG DIEM' // , 1X , 'TT' , 7X, |
| * | 'HO TEN' ,9X , 'D1 D2 D3 TB XEP LOAI' /) |
| C In từng sinh viên theo danh sách | |
| 60 | FORMAT (1X, I2, 1X, A20, I3, I3, I3, F5.1, 1X, 'GIOI') |
| 50 | FORMAT (1X, I2, 1X, A20, I3, I3, I3, F5.1, 1X, 'KHA') |
| 40 | FORMAT (1X, I2, 1X, A20, I3, I3, I3, F5.1, 1X, |
| * | 'TRUNG BINH') |
| I = 1 | |
| 3 | IF (TB (I) .LT. 9.0) THEN |
| IF (TB (I) .LT. 6.0) THEN | |
| PRINT 40 , I , TEN (I) , D1 (I) , D2 (I) , D3 (I) , TB (I) | |
| ELSE | |
| PRINT 50 , I , TEN (I) , D1 (I) , D2 (I) , D3 (I) , TB (I) | |
| END IF | |
| ELSE | |
| PRINT 60 , I , TEN (I) , D1 (I) , D2 (I) , D3 (I) , TB (I) | |
| END IF | |
| I = I + 1 | |
| IF (I. LE. N) GO TO 3 | |
| STOP | |
| END |
Thí dụ 6: Viết chương trình tính tích phân xác định:
theo công thức hình thang với sai số cho trước.
aGợi ý: Ở bước xấp xỉ đầu, xem số hình thang con , tích phân bằng
.
Bước xấp xỉ sau tăng số hình thang con thêm 1 và tích phân bằng (hình 4.3)
Tiếp tục tăng đến khi .

| EPSIL = 0.0001 | |
| A = 0.0 | |
| B = 3.141593 | |
| S1 = 0.5 * (A ** 2 * SIN (A) + B ** 2 * SIN (B)) * (B-A) | |
| SOHINH = 2.0 | |
| 7 | DX = (B-A) / SOHINH |
| HINH = 1.0 | |
| X1 = A | |
| Y1 = X1 ** 2 * SIN (X1) | |
| S2 = 0.0 | |
| 5 | X2 = X1 + DX |
| Y2 = X2 ** 2 * SIN (X2) | |
| S2 = S2 + 0.5*(Y1 + Y2) * DX | |
| IF (HINH .LT. SOHINH) THEN | |
| HINH = HINH + 1.0 | |
| X1 = X2 | |
| Y1 = Y2 | |
| GOTO 5 | |
| END IF | |
| IF (ABS (S2-S1) .GT. EPSIL) THEN | |
| SOHINH = SOHINH + 1.0 | |
| S1 = S2 | |
| GOTO 7 | |
| END IF | |
| PRINT 3 , S2 | |
| 3 | FORMAT (1X , 'TICH PHAN BANG', F15.4) |
| END |
Thí dụ 7: Vòng lặp để tính tổng chuỗi. Bình phương của sin của góc tính theo công thức chuỗi như sau:
.
Hãy viết chương trình đọc vào một góc bằng độ, đổi ra rađian, tính và in ra bảng so sánh kết quả tính theo công thức này với những số số hạng chuỗi lẻ từ 1 đến 15. Thấy rằng số hạng đầu khi là , mỗi số hạng tiếp sau bằng số hạng trước nhân với .
Trong thí dụ này, ta ứng dụng phương pháp chia khối bài toán và chi tiết hóa từng khối như đã trình bày trong mục 4.1 để xây dựng thuật giải và diễn đạt thuật giải đó bằng lưu đồ, sau đó dẫn chương trình Fortran.
Thấy rằng bài toán có thể chia thành ba khối sau:
Khối 1: Nhập giá trị góc .
Khối 2: In tiêu đề của bảng kết quả.
Khối 3: Tính giá trị theo công thức chuỗi và in ra kết quả khảo sát với số số hạng chuỗi từ 1 đến 15.
Bây giờ ta phân tích chi tiết từng khối để dẫn lưu đồ thực hiện trong mỗi khối.
Thấy rằng khối 1 có thể chi tiết hóa thành ba bước con: Vì công thức khai triển chuỗi trên đây hội tụ nhanh đối với những góc nhỏ, do đó nếu nằm trong khoảng:
ta thay bằng góc ,
nếu nằm trong khoảng:
ta thay bằng góc ,
nếu nằm trong khoảng:
ta thay bằng góc .
Sau đó đổi thành rađian (hình 4.4).


Ta thấy khối 2 chỉ gồm hai việc tuần tự là in dòng tiêu đề của bảng khảo sát, in các tiêu đề đầu bảng (hình 4.5).

Khối 3 là phức tạp nhất cần được chi tiết hóa một cách tối đa. Ta thấy khối này gồm các bước cụ thể sau:
Gán 0 cho biến S (giá trị khởi tạo của cần tính).
Gán 1 cho N (bắt đầu xét số hạng thứ nhất).
Gán cho biến THEM (giá trị của số hạng thứ nhất).
Chừng nào thực hiện tuần tự 4 bước sau:
Cộng số hạng (THEM) vào biến S.
Nếu lẻ in giá trị (tính theo hàm chuẩn).
Tăng thêm 1 đơn vị cho .
Tính lại biến THEM bằng cách nhân chính nó với .
Giả trình này tương đương với lưu đồ khối trên hình 4.6.
Như vậy, ta đã chi tiết hóa tất cả các bước trong ba khối dưới dạng các lưu đồ. Công việc còn lại đơn giản là gắn cơ học ba lưu đồ lại ta được lưu đồ chung của toàn thuật toán. Từ đó dễ dàng chuyển sang chương trình Fortran dưới đây:
| PRINT * , ' HAY CHO MOT GOC BANG DO' | |
| READ *, X | |
| IF (X .GT. 90.0) THEN | |
| IF (X .GT. 270.0) THEN | |
| X = X - 360.0 | |
| ELSE IF (X .GT. 180.0) THEN | |
| X = X - 180.0 | |
| ELSE | |
| X = 180.0 - X | |
| END IF | |
| END IF | |
| X = X * 3.141593 / 180.0 | |
| PRINT 2 | |
| 2 | FORMAT (1X, 35H KHAO SAT CONG THUC BINH |
| * | PHUONG SIN // , 1X , 2H N, 17H THEO CONG THUC, |
| * | 17H THEO HAM CHUAN) |
| S = 0. | |
| N = 1 | |
| THEM = X ** 2 | |
| 5 | S = S + THEM |
| IF (MOD (N , 2) .EQ. 1) PRINT 4 , N , S , SIN (X) ** 2 | |
| 4 | FORMAT (1X , I2 , 2F17.7) |
| N = N + 1 | |
| THEM = - THEM * 2.0 * X**2 / (N * (2 * N -1)) | |
| IF (N .LE. 15) GO TO 5 | |
| END |
Thí dụ 8: Nội suy tuyến tính chuỗi số liệu quan trắc. Giả sử có những số liệu quan trắc về nhiệt độ nước biển tại các tầng sâu ở điểm có tọa độ 120oKĐ-20oVB được cho trong bảng 4.3. Lập chương trình nhập những số liệu này và nội suy giá trị nhiệt độ cho một độ sâu bất kỳ nhập từ bàn phím, thông báo lên màn hình kết quả nội suy dưới dạng như sau:
DO SAU = .... M
NHIET DO = ..... DO C
Phân tích bài toán này, ta thấy có thể chia nó thành ba khối: 1) Nhập từ bàn phím một giá trị độ sâu tại đó cần nội suy nhiệt độ; 2) Nhập số liệu về độ sâu và nhiệt độ vào máy tính; 3) Nội suy giá trị nhiệt độ tại độ sâu cần tìm và in kết quả lên màn hình.
Khối thứ nhất rất đơn giản và quen thuộc. Để thực hiện khối thứ hai ta tổ chức một vòng lặp để tuần tự nhập độ sâu và nhiệt độ tại các điểm nút (xem lưu đồ của khối 2 trên hình 4.7).
| Độ sâu | 0 | 5 | 10 | 20 | 30 | 40 | 50 | 60 |
| Nhiệt độ | 24,31 | 24,26 | 24,20 | 24,18 | 24,13 | 24,05 | 23,98 | 23,89 |
| Độ sâu | 70 | 80 | 90 | 100 | 120 | 140 | 160 | 180 |
| Nhiệt độ | 23,87 | 23,57 | 23,14 | 22,74 | 21,31 | 20,03 | 18,49 | 17,58 |
| Độ sâu | 200 | 220 | 240 | 260 | 280 | 300 | 350 | 400 |
| Nhiệt độ | 16,66 | 15,61 | 14,73 | 13,97 | 13,47 | 12,93 | 11,40 | 10,18 |
| Độ sâu | 500 | 600 | 700 | 800 | 900 | 1000 | 1200 | 1400 |
| Nhiệt độ | 9,39 | 8,56 | 8,49 | 7,83 | 7,27 | 6,71 | 6,16 | 5,44 |

Bây giờ ta cụ thể hóa thêm khối thứ 3 và sau đó dẫn chương trình Fortran hoàn chỉnh của bài toán này.
Như đã thấy, các giá trị quan trắc nhiệt độ được cho chỉ tại 32 độ sâu gọi là 32 điểm nút. Muốn nội suy giá trị nhiệt độ tại độ sâu bất kỳ ta cần tìm xem độ sâu đó nằm giữa hai nút nào. Gọi độ sâu cần nội suy nhiệt độ là . Giả sử độ sâu này nằm giữa các độ sâu nút và , tức thỏa mãn bất đẳng thức kép:
,
trong đó có thể biến thiên từ 1 đến 31. Như vậy, để tìm , ta phải giả sử và kiểm tra bất đẳng thức kép trên đây. Nếu bất đẳng thức không thỏa mãn, thì ta tăng lên một đơn vị và tiếp tục cho tới khi bất đẳng thức thỏa mãn.
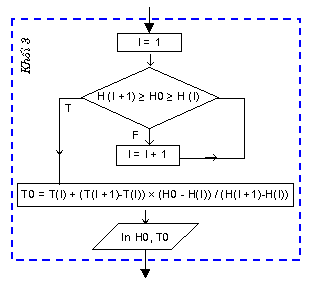
Khi tìm được , giá trị cần nội suy có thể tính theo công thức nội suy tuyến tính như sau:
.
Tất cả những điều vừa phân tích được thể hiện trên lưu đồ khối ở hình 4.8. Dưới đây là chương trình của bài toán
| INTEGER N, I, K | |
| REAL H0, T0, H (40), T (40) | |
| C | In lời nhắc và nhập độ sâu cần nội suy nhiệt độ |
| PRINT * , ' NHAP DO SAU XAC DINH NHIET DO' | |
| READ *, H0 | |
| C | In lời nhắc và nhập 32 cặp giá trị độ sâu và nhiệt độ |
| N = 32 | |
| K = 1 | |
| 5 | PRINT *, ‘ NHAP DO SAU VA NHIET DO TANG ‘, K |
| READ *, H(K), T(K) | |
| K = K +1 | |
| IF (K .GT. N) GOTO 4 | |
| GOTO 5 | |
| C | Nội suy giá trị nhiệt độ tại độ sâu H0 |
| 4 | I = N - 1 |
| IF (H0 .GT. H(N)) GOTO 1 | |
| I = 1 | |
| 2 | IF (H0 .GE. H (I) .AND. H0 .LE. H (I+1)) GOTO 1 |
| I = I + 1 | |
| GOTO 2 | |
| 1 | T0 = T(I) + (T(I+1)-T (I))*(H0-H(I)) / (H(I+1)-H(I)) |
| PRINT 3, H0 | |
| PRINT 6, T0 | |
| 3 | FORMAT (1X, ‘DO SAU = ‘, F6.1, ‘ M’) |
| 6 | FORMAT (1X,’NHIET DO = ‘, F5.1, ’ DO C’) |
| END |
Qua thí dụ ở mục 4.1.3 và những thí dụ ở chương này ta thấy việc áp dụng quy trình 5 bước giải bài toán và chiến lược chia khối và chi tiết hóa từng khối để phát triển thuật giải là một công cụ lập trình rất hiệu quả. Bài toán dù lớn, có cấu trúc phức tạp cũng trở nên sáng tỏ, trực quan.
Từ thời điểm này sinh viên cần rèn luyện cho mình thói quen áp dụng phương pháp trên ngay cả với những bài tập đơn giản cũng như với những bài toán tương đối phức tạp khi thiết kế thuật giải. Còn chọn công cụ giả trình hay lưu đồ là tùy thích.
Bài tập
1. Hãy thể hiện bằng giả trình hoặc lưu đồ thuật toán sắp xếp các phần tử của mảng một chiều theo thứ tự giảm dần.
2. Cho các giá trị:
Xác định giá trị của các biểu thức lôgic sau đây:
1) A .LT. B 2) A - B .GE. 6.5
3) I .NE. 5 4) A + B .GE. B
5) I .LE. I -5 6) .NOT. (A .EQ. 2 * B)
7) (A .LT. 10.0) .AND. (B .GT. 5.0)
8) (ABS (I) .GT. 2) .OR. DONE
9) A .LT. B .NEQV. DONE
3. Viết chương trình tính giá trị của theo công thức
với cho trước.
4. Viết chương trình đọc từ bàn phím một trị số nhiệt độ Celsius, liệt kê trên màn hình ba phương án chuyển đổi: sang độ Fahrenheit, Kelvin và Rankin. Theo người dùng chỉ định phương án chuyển đổi mà in ra nhiệt độ đã cho và kết quả chuyển đổi kèm các ký hiệu nhiệt độ tương ứng. Các công thức chuyển đổi như sau:
5. Viết chương trình tính tích phân với hàm cho dưới dạng bảng các giá trị thực nghiệm như trong bảng 4.4.
Bảng 4.4
| 1,0 | 2,1 | 3,0 | 3,9 | 4,8 | 6,2 | 7,1 | 7,8 | |
| 3,3 | 4,7 | 7,3 | 8,7 | 11,3 | 12,7 | 15,3 | 16,7 | |
| 9,4 | 10,1 | 11,3 | 12,1 | 13,5 | 13,9 | 15,0 | ||
| 19,3 | 20,7 | 23,3 | 24,7 | 27,3 | 28,7 | 31,3 |
6. Viết chương trình cho phép đọc vào từ bàn phím một trị số của và xác định trị số của hàm bằng cách nội suy tuyến tính theo bảng giá trị thực nghiệm (thí dụ bảng 4.4).
7. Hệ số nhớt phân tử ( ) của nước biển phụ thuộc vào nhiệt độ (°) và độ muối (%o) theo bảng 4.5. Viết chương trình nội suy tuyến tính bảng này cho một cặp trị số bất kỳ của và .
8. Viết chương trình tính số theo công thức khai triển chuỗi sau đây với sai số không quá 0,0001:
Bảng 4.5
| Độ muối | 0° | 5° | 10° | 15° | 20° | 25° | 30° |
| 0 | 17,94 | 15,19 | 13,10 | 11,45 | 10,09 | 8,95 | 8,00 |
| 5 | 18,06 | 15,28 | 13,20 | 11,54 | 10,18 | 9,08 | 8,09 |
| 10 | 18,18 | 15,39 | 13,28 | 11,68 | 10,27 | 9,18 | 8,17 |
| 15 | 18,30 | 15,53 | 13,41 | 11,77 | 10,40 | 9,26 | 8,27 |
| 20 | 18,41 | 15,66 | 13,57 | 11,90 | 10,47 | 9,35 | 8,34 |
| 25 | 18,53 | 15,79 | 13,73 | 12,03 | 10,58 | 9,48 | 8,43 |
| 30 | 18,64 | 15,93 | 13,84 | 12,12 | 10,68 | 9,58 | 8,52 |
| 35 | 18,83 | 16,07 | 14,00 | 12,23 | 10,82 | 9,67 | 8,59 |
9. Viết chương trình cho phép liên tục nhập từ bàn phím hai số nguyên bất kỳ, tìm và in lên màn hình ước số chung lớn nhất của những số đó dưới dạng thông báo:
USCLN CUA CAC SO: 36 VA 24 BANG 12
và kết thúc khi nào người dùng nhập vào hai số bằng nhau hoặc một trong hai số bằng 1.
10. Lập lưu đồ thuật giải để giải gần đúng phương trình bằng phương pháp lặp Siedel. Xấp xỉ ban đầu và sai số cho phép được cho trước. Nếu tìm được nghiệm với độ chính xác đã cho thì in giá trị nghiệm kèm theo số bước lặp, còn nếu sau 100 lần lặp mà chưa nhận được nghiệm thì thông báo lên màn hình dòng chữ 'KHONG TIM DUOC NGHIEM'. (Gợi ý: Theo phương pháp lặp Seidel, người ta thế giá trị tùy chọn vào biểu thức ở vế phải của phương trình để tính ra giá trị gọi là xấp xỉ bậc 1, sau đó kiểm tra nếu khác nhau giữa và lớn hơn sai số cho phép thì giá trị lại được thế vào vế phải và tiếp tục tính (xấp xỉ bậc 2)..., quá trình này tiếp diễn cho đến khi chênh lệch giữa hai bước xấp xỉ liền nhau không lớn hơn thì người ta chấp nhận giá trị xấp xỉ cuối cùng làm nghiệm của phương trình .