Phạm Văn Huấn
Trường ĐHTH Hà Nội
Lý thuyết các dao động tự do trong những thủy vực hở một phần hoặc kín hoàn toàn dựa trên phép xấp xỉ kênh, khi chuyển động diễn ra chủ yếu theo một hướng. Đối với những thủy vực hình dáng đơn giản, chẳng hạn, có thể sử dụng công thức Merian để tính các giá trị của chu kỳ dao động tự do cho cả thủy vực hoặc từng phần của nó rồi sau đó ghép nối cho toàn thủy vực.
Trong biển thực mà đặc trưng là sự tồn tại đường bờ phức tạp với những eo, vịnh, đảo và bán đảo, những bất đồng nhất độ sâu, thềm lục địa, sẽ diễn ra những quá trình phản xạ, phát xạ sóng và trong biển sẽ hình thành một chế độ dao động tự do phức tạp, khác nhau ở những điểm khác nhau. Trong trường hợp này có thể nghiên cứu chế độ cộng hưởng dựa trên những quan trắc mực nước. Đánh giá triều riêng bằng bằng cách so sánh những quan trắc nhiều năm của mực nước ở các quần đảo Axo và Becmuda với triều tĩnh đã cho phép phân biệt những chu kỳ cộng hưởng của Bắc Đại Tây Dương bằng 9,3 và 14,8 giờ [8]. Haret [3] đã thử tính các chu kỳ riêng của hệ thống vịnh Phandi-Men trên cơ sở phân tích sự khuếch đại của từng sóng thủy triều ở những khu vực bờ khác nhau và nhận được chu kỳ cộng hưởng bằng giờ.
Một phương pháp khác để tính tới độ sâu và hình dáng tự nhiên của biển là phương pháp tích phân bằng số những phương trình Laplat không ma sát trong khuôn khổ bài toán biên không dừng khi kích động những dao động riêng bởi nhiễu động ban đầu bất kỳ. Phân tích phổ các chuỗi mực nước tính được sẽ cho phép tìm những tần số riêng (những chu kỳ riêng), còn phân tích điều hòa - những hàm riêng (những mốt).
Để giải bài toán đối với biển Đông, chúng tôi sử dụng phương pháp đã nêu với sơ đồ tính đã được xây dựng trong các công trình [6, 1, 7, 4] khi nghiên cứu các dao động tự do của các biển Liguri, Hắc Hải, Bắc Băng Dương và đại dương thế giới nói chung.
Các phương trình xuất phát là những phương trình nước nông không kể ma sát viết dưới dạng ma trận:
(1)
với những điều kiện ban đầu và biên:
(2)
(3)
(4)
trong đó hàm vectơ, vectơ các dòng toàn phần, độ cao mực nước, toán tử vi phân xác định bằng
,
với những vectơ đơn vị hướng tuần tự thẳng đứng lên trên và pháp tuyến với vành bờ, vành bờ cứng, biên lỏng, nhiễu động ban đầu của trường mực nước, độ sâu biển, thông số Coriolit, gia tốc rơi tự do.
Trong hệ trên, sự có mặt của trong toán tử cho phép tính đến đầy đủ động lực vùng nước nông, điều kiện (4) loại mất phần tần thấp trong phổ những dao động tự do có thể có trong biển Đông như là một bộ phận của Thái Bình Dương.
Để giải bằng số bài toán (1)-(4) toàn bộ biển Đông được xấp xỉ bằng mạng lưới với bước dọc theo các trục tọa độ bằng một độ kinh và vĩ. Phần biên cứng là toàn bộ bờ của các nước xung quanh, những eo biển hẹp xen kẽ với những chuỗi đảo nhỏ. Chỉ riêng ở phía đông và bắc, eo Đài Loan và eo Luxông với độ sâu ở giữa tuần tự cỡ 100 mét và hơn 3000 mét được coi là biên lỏng. Các trị được tính ở các điểm xê dịch nhau một nửa bước lưới [2]. Các đạo hàm không gian được thay bằng những tương tự sai phân hữu hạn trung tâm, các trị của và tại từng bước thời gian về phía tương lai (bằng 150 giây) được tính với độ chính xác bậc bốn của chuỗi Taylo.
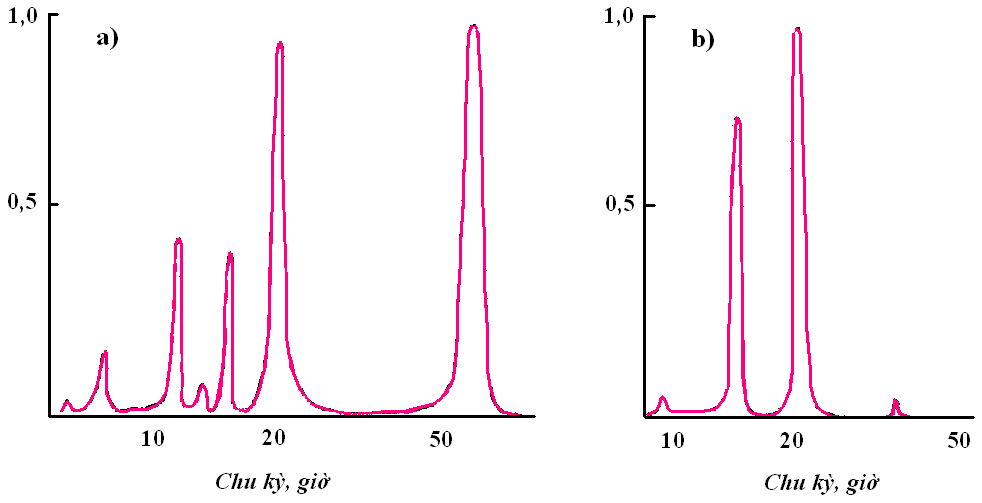
Độ dài các chuỗi trị số mực nước tính được dùng để nhận phổ các dao động tự do bằng 1000 với độ gián đoạn bằng 1 giờ.
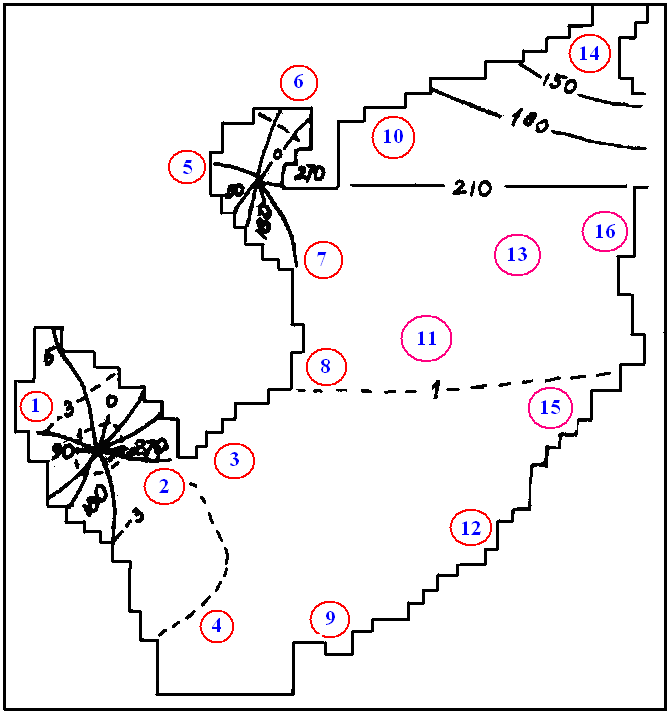
Tất cả các phổ những dao động tự do được xây dựng cho 16 điểm phân bố đều dọc theo các bờ và phần khơi (xem vị trí của các điểm trên hình 2) có tính gián đoạn rõ rệt (thí dụ phổ của điểm 1 thuộc vịnh Thái Lan và điểm 6 thuộc vịnh Bắc Bộ trên hình 1a và 1b) và trong dải chu kỳ từ 1 đến 60 giờ chúng tôi đã phân biệt được 15 dao động (mốt) tự do với năng lượng đáng kể là 60, 24, 19,2, 17,2, 14,7, 14,3, 13,2, 11,6, 10,6, 9,7, 9,4, 7,6, 7,1, 6,1 và 4,2 giờ. Những vùng khác nhau của biển, ngoài những mốt chung với toàn biển là 24 và 19,2 giờ, còn có những mốt địa phương, thí dụ ở vịnh Thái Lan có mặt những mốt với chu kỳ 60, 14,7, 11,6, 10,6 và 9,7 giờ, ở vịnh Bắc Bộ – 17,2 và 14,3 giờ, vùng bờ sâu tiếp giáp miền Trung Việt Nam và ngoài biển khơi – 17,2 giờ.
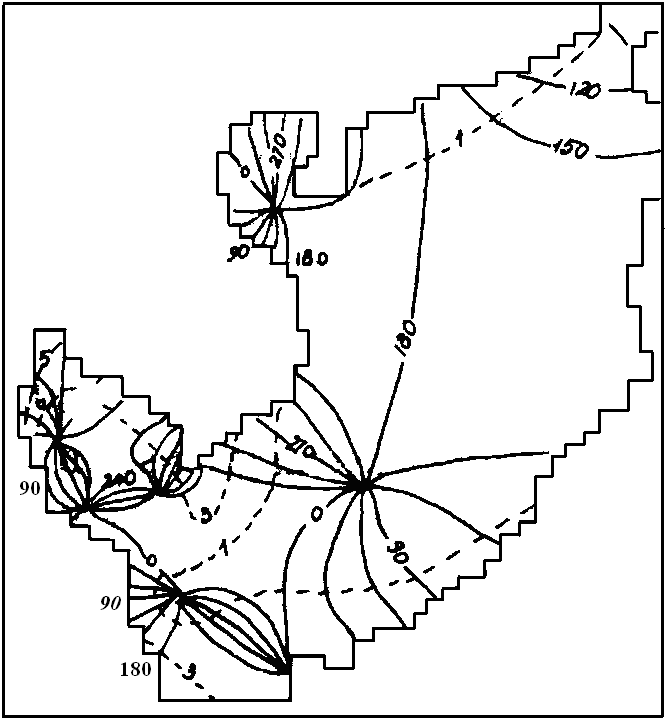
Để tái lập cấu trúc không gian của các mốt đã xây dựng các bản đồ đường đồng pha và đồng biên độ của bảy mốt tuần tự ứng với các chu kỳ 60, 24, 19,2, 17,2, 11,6, 10,6 và 9,7 giờ. Các hình 2 và 3 là những thí dụ về các bản đồ kiểu ấy. Nét nổi bật trên tất cả các bản đồ là tồn tại các hệ thống rốn triều quay ngược chiều kim đồng hồ. Những biên độ lớn nhất thấy ở các vùng nước nông, đặc biệt ở những đỉnh vịnh.
Những tính toán trên đây là kết quả đầu tiên về ước lượng mô hình những chu kỳ dao động tự do của biển Đông, có thể sử dụng để phân vùng thủy vực này theo đặc điểm dao động tự do, giải thích những đặc điểm dao động triều vốn rất đặc biệt ở đây, hoặc chỉ ra khả năng phản ứng cộng hưởng của từng đới bờ đối với những kích động từ bên ngoài như những dao động khí quyển khi nghiên cứu biến động mực nước.
Theo tư tưởng vừa nêu có thể sơ bộ chia biển thành sáu vùng với khả năng phản ứng khác nhau, nói theo ngôn ngữ kỹ thuật, những bộ cộng hưởng khác nhau như sau:
Vùng I gồm thềm lục địa tây nam biển, vịnh Thái Lan trừ dải hẹp cận bờ đông (giáp Nam Việt Nam) với chế độ dao động phức tạp nhất, phản ứng cộng hưởng với những kích động trong dải chu kỳ rộng từ vài ngày, ngày, nửa ngày cho đến các chu kỳ gọi là nước nông. Biên độ dao động lớn nhất.
Vùng II là nửa phía tây vịnh Bắc Bộ với chế độ dao động thuần nhất hơn, chỉ cộng hưởng với các chu kỳ ngày, nửa ngày và nước nông. Biên độ dao động tương đối lớn.
Vùng III là nửa đông và bắc vịnh Bắc Bộ chỉ khác vùng II bởi chỗ chu kỳ ngày áp đảo hơn hết. Biên độ dao động lớn.
Vùng IV rộng lớn nhất, gồm toàn bộ thủy vực biển từ bờ tây đông phản ứng với chu kỳ ngày và biên độ dao động nhỏ.
Vùng V là dải ven bờ tây bắc biển (ven bờ Trung Quốc) và vùng VI là thềm lục địa nam đông nam biển có đặc điểm như vùng IV cộng với khả năng phản ứng với các dao động nước nông. Biên độ dao động trung bình.
Kết quả tính và phân tích như trên khá phù hợp với những giải thích về chuyển động triều ở biển Đông và các vịnh Bắc Bộ, Thái Lan. Nếu có điều kiện so sánh với những biến động dao động của các tác nhân bên ngoài như các yếu tố khí tượng, hoàn lưu khí quyển... thì có thể nghiên cứu chế độ biến động mực nước biển dưới góc độ tương tác cộng hưởng, xác định cơ chế tương tác, điều rất có ý nghĩa trong khi dự báo dao động mực nước biển.
TÀI LIỆU THAM KHẢO
1. Đemirov E.K. Giải bằng số bài toán dao động riêng ở Hắc Hải/ Okeanologia, 1987, 27, N5.
2. Đỗ Ngọc Quỳnh. Đặc điểm nước dâng trong bão ở biển Nam Trung Hoa (theo kết quả mô hình bằng số). Luận án PTS, 1982, Trường ĐHKTTV Lêningrát.
3. Garrette C.J. Normal modes of the Bay of Fundy and the Gulf of Maine/ Can. J. Earth Sci., 1974, 11, N4.
4. Gotlib V.Iu., Kagan B.A. Những chu kỳ cộng hưởng ở Đại dương Thế giới/ Báo cáo VHLKH Liên Xô, 1980, 253, N3. Tái lập cấu trúc không gian của nhật triều ở Đại dương Thế giới dựa trên các hàm riêng của toán tử triều Laplat/ Okeanologia, 1983, tập 23, số 4.
5. Nhecraxov A.V. Những sóng triều ở các biển ven. Nxb Giđrometeoizdat, Lêningrát, 1975.
6. Papa L. The free oscillations of Ligurian sea computed by HN-method/ Dtsch Hydrogr., 1977, 3OH3.
7. Poliacov I.V. Những cơ chế hình thành dao động dâng rút mực nước các biển Bắc Cực/ Luận án PTS, 1989, Trường ĐHKTTV Lêningrát.
8. Wunsch C. Bermuda sea level in relation to tides, wheather and bar clinic fluctuations/ Rev. Geogr. Geophys. and Space Phys., 1972, 10, N1.
SUMMARY
THE FREE OSCILLATIONS AND THE RESONANCE IN THE OSCILLATION
OF EAST SEA LEVEL
Pham Van Huan
Hanoi University
The long wave equations of shallow water are solved by a finite difference method for South-china sea with real morphology and bathymetry. In result, 15 modes of free oscillations are determined and the space forms of 7 modes among them are reconstructed. This all permitted to divide the sea into six districts with different ways to respond to external forces.