INTRODUCTION
In electrical engineering we are often interested in communicating or transferring energy from one point to another. To do this requires an interconnection of electrical devices. Such interconnection is referred to as an electric circuit, and each component of the circuit is known as an element.
An electric circuit is an interconnection of electrical elements.
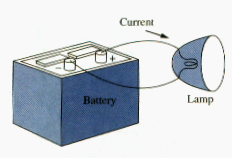
A simple electric circuit is shown in [link]. It consists of three basic elements: a battery, a lamp, and connecting wires.
SYSTEM OF UNITS
As electrical engineers, we deal with measurable quantities. Our measurement, however, must be communicated in a standard language that virtually all professionals can understand. Such an international measurement language is the International System of Units (SI), adopted by the General Conference on Weights and Measures in 1960. In this system, there are six principal units from which the units of all physical quantities can be derived. [link] shows the six units, their symbol, and the physic quantities they represent. The SI units are used throughout this text.
| Quantity | Basic unit | Symbol |
| Length | meter | m |
| Mass | kilogram | kg |
| Time | second | s |
| Electric current | ampere | A |
| Thermodynamic temperature | kelvil | K |
| Luminous intensity | candela | cd |
One great advantage of the SI unit is that it uses prefixes based on the power of 10 to relate larger and smaller units to the basic unit. [link] shows the SI prefixes and their symbols. For example, the following expressions of the same distance in meters (m):
600.000.000 mm600.000 m600 km
| Multiplier | Prefix | Symbol |
| exa | E | |
| peta | P | |
| tera | T | |
| giga | G | |
| mega | M | |
| kilo | k | |
| hecto | h | |
| 10 | deka | da |
| deci | d | |
| centi | c | |
| mili | m | |
| micro | ||
| nano | n | |
| pico | p | |
| femto | f | |
| atto | a |
CHARGE AND CURRENT
The concept of electric charge is underlying principle for explaining electrical phenomena. Also, the most basic quantity in an electric circuit is the electric charge. We all experience the effect of electric charge where we try to remove our wool sweater and have it stick to our body or walk across a carpet and receive a shock.
Charge is an electrical property of the atomic particle of which matter consists, measured in coulomb (C).
We know from elementary physics that all matter is made of fundamental building blocks known as atoms and that each atom consists electrons, protons and neutrons. We also know that the charge e on an electron is negative and equal in magnitude to , while a proton carries a positive charge of the same magnitude as the electron. The presence of equal numbers of protons and electrons leaves an atom neutrally charged.
The following points should be noted about electric charge:
- The Coulomb is a large unit for charges. In 1 C of charge, there are electrons. Thus realistic or laboratory values of charges are on the order of pC, nC, or C.
- According to experimental observations, the only charges that occur in nature are integral multiples of electronic charge .
- The law of conservation of charge states that charge can neither be created nor destroyed only transferred. Thus the algebraic sum of the electric charges in a system does not change.
We now consider the flow of electric charges. A unique feature of electric charge or electricity is the fact that it is mobile; that is, it can be transferred from one place to another, where it can be converted to another form of energy.
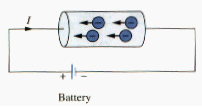
When a conducting wire (consisting of several atoms) is connected to a battery (a source of electromotive force), the charges are completed to move; positive charges move to one direction while negative charges move in opposite direction. This motion of charges creates electric current. It is conventional to take the current flow as the movement of positive charges, that is, opposite to the negative charges. As [link] illustrates. This convention was introduced by Benjamin Franklin (1706-1790), the American scientist and inventor. Although we know that current in metallic conductors is due to negatively charged electrons, we will follow the universally accepted convention that current is the net flow of positive charges. Thus,
Electric current is the time rate of change of charge, measured in amperes (A).
Mathematically, the relationship between current i, charge q, and time t is
Where current is measured in amperes (A), and
1 ampere = 1 coulomb/second
The charge transferred between time to t is obtained by integrating both sides of [link]. We obtain
The way we define current I in [link] suggests that current need not be a constant-valued function. There can be several types of current; that is, charge can vary with time in several ways.
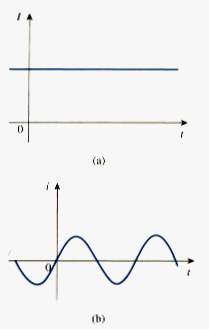
If the current does not change with time, but remains constant, we call it a direct current (dc).
A direct current (dc) is a current that remains constant with time.
By convention the symbol I is used to represent such a constant current.
A time varying current is represented by a symbol i. a common form of time-varying is the sinusoidal current or alternating current (ac).
An alternating current (ac) is a current that varies sinusoidally with time.
Such current is used in your household, to run air conditioner, refrigerator, washing machine, and other electric appliances. [link] shows direct current and alternating current; these are the two most common types of current.
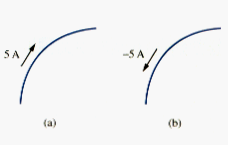
Once we define current as the movement of charge, we expect current to have an associated direction of flow. As mentioned earlier, the direction of current flow is conventionally taken as the direction of the positive charge movement. Based on this convention, a current of 5A may be represented positively or negatively as shown in [link]. in other word, a negative current of -5 A flowing in one direction as shown in [link](b) is the same as a current of + 5A flowing in the opposite direction.
VOLTAGE
As explained briefly in the previous section, to move the electron in a conductor in a particular direction requires some work or energy transfer. This work is performed by an external electromotive force (emf), typically represented by the battery in [link]. This emf also known as voltage or potential difference. The voltage between two points a and b in an electric current is the energy (or work) needed to move a unit charge from a to b; mathematically,
Where w is energy in joules (J) and q is charge in coulombs (C). The voltage or simply v is measured in volts (V), named in honor of the Italian physicist Alessandro Antonio Volta (1745-1827), who invented the first voltaic battery. From [link], it is evident that
1 volt = 1 joule/coulomb = 1 newton meter/coulomb
Thus,
Voltage (or potential difference) is the energy required to move a unit charge through an element, measured in volts (V).
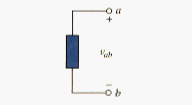
[link] shows the voltage across an element (represented by rectangular block) connected to points a and b. The plus (+) and minus (-) signs are used to define reference direction or voltage polarity. The can be interpreted in two ways: 1) point a is at a potential of volts higher than point b, or 2) the potential at point a with respect to point b is . It follows logically that in general
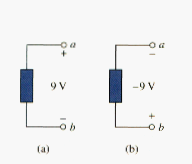
For example, in [link], we have two representations of the same voltage. In [link](a), point a is +9V above point b; in [link](b), point b is -9 V above point a. We may say that in [link](a), there is a 9V voltage drop from a to b or equivalently a 9V voltage rise from b to a. In the other words, a voltage drop from a to b is equivalent to a voltage rise from b to a.
Current and voltage are the two basic variables in electric circuits. The common term signal is used for an electric quantity such as a current or a voltage (or electromagnetic wave) when it is used for conveying information. Engineers prefer to call such variable signals rather than mathematical functions of time because of their importance in communications and other disciplines. Like electric current, a constant voltage is called a dc voltage and is represented by V, whereas a sinusoidal time-varying voltage is called an ac voltage and is represented by v. A dc voltage is commonly produced by a battery; ac voltage is produced by an electric generator.
POWER AND ENERGY
Although current and voltage are the two basic variables in an electric circuit, they are not sufficient by themselves. For practical purposes, we need to know how much power an electric device can handle. We all know from experience that a 100-watt bulb gives more light than a 60-watt bulb. We also know that when we pay our bills to the electric utility companies, we are paying for the electric energy consumed over a certain period or time. Thus power and energy calculations are important in circuit analysis.
To relate power and energy to voltage and current, we recall from physics that:
Power is the time rate of expending or absorbing energy, measured in watts (W).
We write this relationship as
Where p is power in watts (W), w is energy in joules (J), and t is time in seconds (s). From [link] and [link], it follows that
or
The power in [link] is a time-varying quantity and is called the instantaneous power. Thus, the power absorbed or supplied by an element is the product of the voltage across the element and the current through it. If the power has a + sign, power is being delivered to or absorbed by the element, if, on the other hand, the power has a – sign, power is being supplied by the element. But how do we know when the power has a negative or a positive sign?
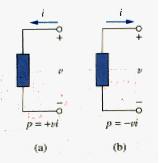
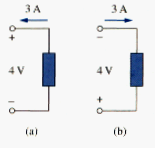
Current direction and voltage polarity play a major role in determining the sign of power. It is therefore important that we pay attention to the relationship between current I and voltage v in [link](a). The voltage polarity and current direction must confirm with those shown in [link](a) in order for the power to have a positive sign. This is known as the passive sign convention. By the passive sign convention, current enters through the positive polarity of the voltage. In this case, p = + vi or vi > 0 implies that the element is absorbing power. However, if p = - vi or vi < 0, as in [link]((b), the element is releasing or supplying power.
Passive sign convention is satisfied when the current enters through the positive terminal of an element and p = + vi. If the current enters through the negative terminal, p = - vi.
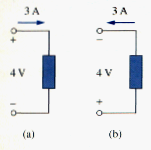
Unless otherwise stated, we will follow the passive sign convention throughout this text. For example, the element in both circuits of [link] has an absorbing power of + 12 W because a positive current enters the positive terminal in both cases. In [link], however, the element is supplying power of +12 W because a positive current enters negative terminal. Of course, an absorbing power of – 12 W is equivalent to a supplying power of + 12 W. In general,
+ Power absorbed = - Power supplied
In fact, the law of conservation of energy must be obeyed in any electric circuit. For this reason, the algebraic sum of power in a circuit, at any instant of time, must be zero:
This again confirms the fact that the total power supplied to the circuit must balance the total power absorbed.
From [link], the energy absorbed or supplied by an element from time t0 to time t is
Energy is the capacity to do work, measured in joules (J).
The electric power utility companies measure energy in watt-hours (Wh), where
1 Wh = 3,600 J
CIRCUIT ELEMENTS
As we discussed in section 1, an element is the basic building block of a circuit. An electric circuit is simply an interconnection of the elements. Circuit analysis is the process of the determining voltage across (or the currents through) the element of the circuit.
There are two types of elements found in electric circuits: passive elements and active elements. An active element is capable of generating energy while a passive element is not. Examples of passive elements are resistors, capacitors, and inductors. Typical active elements include generators, batteries, and operational amplifiers. Our aim in this section is to gain familiarity with some important active elements.
The most important active elements are voltage or current sources that generally deliver power to the circuit connected to them. There are two kinds of the sources: independent and dependent sources.
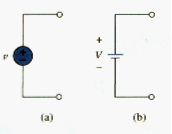
An ideal independent source is an active element that provides a specific voltage or current that is completely independent of other circuit elements.
In other words, an ideal independent voltage source delivers to the circuit whatever current is necessary to maintain its terminal voltage. Physical sources such as batteries and generators may be regarded as approximation to ideal voltage sources. [link] shows the symbol for independent voltage sources. Notice that both symbols in [link](a) and (b) can be used to represent a dc voltage source. Similarly, an ideal independent current source is an active element that provides a specified current completely independent of the voltage across the source. That is, the current source delivers to the circuit whatever voltage is necessary to designated current. The symbol for an independent current source is displayed in [link], where the arrow indicates the direction of the current i.
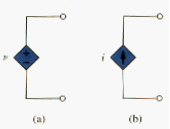
An ideal dependent (or controlled) source is an active element in which the source quality is controlled by another voltage or current.
Dependent sources are designated by diamond shaped symbols, as shown in [link]. Since the control of the dependent source is achieved by a voltage or current of some other element in the circuit, and the source can be voltage or current, it follows that there are four possible types of dependent sources, namely:

- A voltage-controlled voltage source (VCVS).
- A current-controlled voltage source (CCVS).
- A voltage-controlled current source (VCCS).
- A current-controlled current source (CCCS).
Dependent sources are useful in modeling elements such as transistors, operational amplifiers and integrated circuits. An example of a current-controlled voltage source is shown on the right-hand side of [link], where the voltage 10i V of voltage source depends on the current i through element C. Students might be surprised that the value of dependent voltage source is 10i V (and not 10i A) because it is a voltage source. The key idea to keep in mind is that a voltage source comes with polarities (+ -) in its symbol, while a current source comes with an arrow, irrespective of what it depends on.
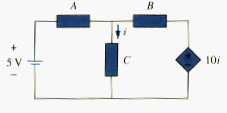
It should be noted that an ideal voltage source (dependent or independent) will produce any current required to ensure that the terminal voltage is as stated, whereas an ideal current source will produce the necessary voltage to ensure the stated current flow. Thus an ideal source could in theory supply an infinite amount of energy. It should also be noted that not only do sources supply power to a circuit, they can absorb power from a circuit too. For a voltage source, we know the voltage but not the current supplied or drawn by it. By the same token, we know the current supplied by a current source but not the voltage across it.
SUMMARY
- An electric circuit consists of electrical elements connected together.
- The International System of Units (SI) is the international measurement language, which enables engineers to communicate their results. From the six principle units, the units of other physical quantities can be derived.
- Current is rate of charge flow.
- Voltage is the energy required to move 1 C of charge through an element.
- Power is energy supplied or absorbed per unit time. It is also the product of voltage and current.
- According to the passive sign conversion, power assumes a positive sign when the current enters the positive polarity of the voltage across an element.
- An ideal voltage source produces a specific potential difference across its terminals regardless of what is connected to it. An ideal current source produces a specific current through its terminals regardless of what is connected to it.
- Voltage and current sources can be dependent or independent. A dependent source is one whose value depends on some other circuit variable.