INTRODUCTION
Chapter 1 introduced basic concepts such as current, voltage, and power in an electric circuit. To actually determine the values of this variable in a given circuit requires that we understand some fundamental laws govern electric circuits. These laws known as Ohm’s law and Kirchhoff’s laws, from the foundation upon which electric circuit analysis is build.
In this chapter, in addition to these laws we shall discuss some techniques commonly applied in circuit design and analysis. These techniques include combining resistors in series or parallel, voltage division, current division and delta-to-wye and wye-to-delta transformations
OHM’S LAW
Materials in general have a characteristic behavior of resisting the flow of electric charge. This physical property or ability to resist current known as resistance and is represented by the symbol R. the resistance of any material with a uniform cross-sectional area A depends on A and its length l, as shown in [link](a). We can represent resistance (as measured in the laboratory), in mathematical form,
where is known as the resistivity of the material in ohm-meters. Good conductors, such as copper and aluminum, have low resistivities, while insulators, such as mica and paper, have high resistivities. [link] presents the values of for some common materials and shows which materials are used for conductors, insulators, and semiconductors.
| Material | Resistivity ( ) | Usage |
| Silver | Conductor | |
| Copper | Conductor | |
| Aluminum | Conductor | |
| Gold | Conductor | |
| Carbon | Semiconductor | |
| Germanium | Semiconductor | |
| Silicon | Semiconductor | |
| Paper | Insulator | |
| Mica | Insulator | |
| Glass | Insulator | |
| Teflon | Insulator |
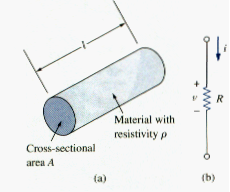
The circuit element used to model the current-resisting behavior of a material is the resistor. For the purpose of constructing circuits, resistors are usually made from metallic alloys and carbon compounds. The circuit symbol for the resistor is shown in [link](b), where R stands for the resistance of the resistor. The resistor is the simplest passive element.
Georg Simon Ohm (1787-1854), a German physicist, is credited with finding the relationship between current and voltage for a resistor. This relationship is known as Ohm’s law.
Ohm’s law states that the voltage v across a resistor is directly proportional to the current i flowing through the resistor.
That is,
Ohm defined the constant of proportionality for a resistor to be the resistance, R. Thus, [link] becomes
Which is the mathematical form of Ohm’s law. R in [link] is measured in the unit of Ohms, designated . Thus,
The resistance R of an element denotes its ability to resist the flow of electric current; it is measured in ohms ( ).
We may deduce from [link] that
So that
1 = 1 V/A
To apply Ohm’s law as stated in [link], we must pay careful attention to the current direction and voltage polarity. The direction of current i and the polarity of voltage v must conform with the passive sign convention, as shown in [link](b). This implies that current flows from a higher potential to a lower potential in order for v = iR. If current flows from a lower potential to a higher potential, v = -iR.
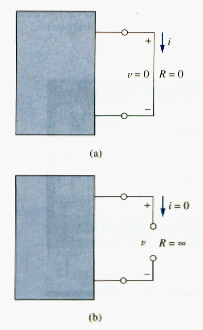
Since the value of R can range from zero to infinity, it is important that we consider the two extreme possible values of R. An element with R = 0 is called a short circuit, as shown in [link](a). For a short circuit,
Showing that the voltage is zero but the current could be anything. In practice, a short circuit is usually a connecting wire assumed to be a perfect conductor. Thus,
A short circuit is a circuit element with resistance approaching zero.
Similarly, an element with R = is known as an open circuit, as shown in [link](b). For an open circuit,
Indicating that the current is zero though the voltage could be anything. Thus,
An open circuit is a circuit element with resistance approaching infinity.

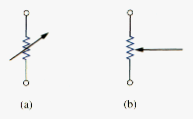
A resistor is either fixed or variable. Most resistors are of the fixed type, meaning their resistance remains constant. The two common types of fixed resistors (wirewound and composition) are shown in [link]. The composition resistors are used when large resistance is needed. The circuit symbol in [link](b) is for a fixed resistor. Variable resistors have adjustable resistance. The symbol for a variable resistor is shown in [link](a). A common variable resistor is known as a potentiometer or pot for short, with the symbol shown in [link](b). The pot is three-terminal element with the sliding contact or wiper. By the sliding wiper, the resistances between the wiper terminal and the fixed terminals vary. Like fixed resistors, variable resistors can either be of wirewound or composition type, as shown in [link]. Although resistors like those in [link] and [link] are used in circuit designs, today most circuit components including resistors are either surface mounted or integrated, as typically shown in [link].

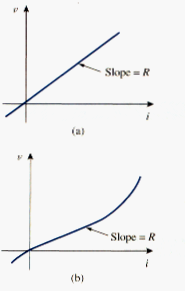
It should be pointed out that not all resistors obey Ohm’s law. A resistor that obeys Ohm’s law is known as a linear resistor. It has a constant resistance and thus its current-voltage characteristic is as illustrated in [link](a): its i-v graph is a strait passing through the origin. A nonlinear resistor does not obey Ohm’s law. Its resistance varies with current and its i-v characteristic is typically shown in [link](b). Examples of devices with nonlinear resistance are the lightbulb and the diode. Although all practical resistors may exhibit nonlinear behavior under certain conditions, we will assume in this book that all elements actually designated as resistors are linear.

A useful quantity in circuit analysis is the reciprocal of resistance R, known as conductance and denoted by G:
The conductance is a measure of how well an element will conduct electric current. The unit of conductance is the siemens (S), the SI unit of conductance:
Thus,
Conductance is the ability of an element to conduct electric current; it is measured in siemens (S).
The same resistance can be expressed in ohms or siemens. For example, 10 is the same as 0.1 S. from [link], we may write
The power dissipated by a resistor can be expressed in term of R. using [link] and [link],
The power dissipated by a resistor may also be expressed in terms of G as
We should note two things from [link] and [link]:
1. The power dissipated in a resistor is a nonlinear function of either current or voltage.
2. Since R and G are positive quantities, the power dissipated in a resistor is always positive. Thus, a resistor always absorbs power from the circuit. This confirms the idea that a resistor is a passive element, incapable of generating energy.
NODES, BRANCHES AND LOOPS
Since the elements of an electric circuit can be interconnected in several ways, we used to understand some basic concepts of network topology. To differentiate between a circuit and a network, we may regard a network as an interconnection of elements or devices, whereas a circuit is a network providing one or more closed paths. The convention, when addressing network topology, is to use the word network and circuit mean the same thing when used in this context. Such elements include branches, nodes, and loops.
A branch represents a single element such as a voltage source or a resistor.
In the other words, a branch represents any two-terminal element. The circuit in [link] has five branches, namely, the 10 V voltage source, the 2 A current source, and the three resistors.
A node is the point of connection between two or more branches.
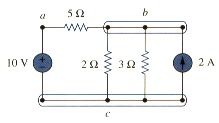
A node is usually indicated by a dot in a circuit. If a short circuit (a connecting wire) connects two nodes, the two nodes constitute a single node. The circuit in [link] has three nodes a, b, and c. notice that the three points that form node b are connected by perfectly conducting wires and therefore constitute a single point. The same is true of the four points forming nodes c. we demonstrate that the circuit in [link] has only three nodes by redrawing the circuit in [link]. The two circuits in [link] and [link] are identical. However, for the sake of the clarity, nodes b and c are spread out with perfect conductors as in [link].
A loop is any closed path in a circuit.
A loop is a closed path formed by starting at a node, passing through any node more than one. A loop is said to be independent if it contains at least one branch which is not a part of any other independent loop. Independent loops or paths result in independent sets of equations.
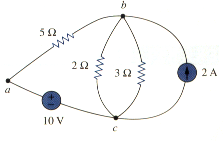
For example, the closed path abca containing the 2- resistor in [link] is a loop. Another loop is the closed path bcb containing the 3- resistor and current source. Although one can identify six loops in [link], only three of them are independent.
A network with b branches, n nodes, and l independent loops will satisfy the fundamental theorem of network topology:
b = l + n - 1
As the next two definitions show, circuit topology is of great value to the study of voltages and currents in an electric circuit.
Two or more elements in series if they exclusively share a single node and consequently carry the same current.
Two more elements are in parallel if they are connected to the same two nodes and consequently have the same voltage across them.
Elements are in series when they are chain-connected or connected sequentially, end to end. For example, two elements are in series if they share one common node and no other element is connected to that common node. Elements in parallel are connected to the same pair of terminals. Elements may be connected in a way that they are neither in series nor in parallel. In the circuit show in [link], the voltage source and the 5- resistor are in series because the same current will flow through them. The 2- resistor, the 3- resistor, and the current source are in parallel because they are connected to the same two nodes (b and c) resistors and neither in series nor in parallel with each other.
KIRCHHOFF’S LAWS
Ohm’s law is not sufficient to analyze circuits. However, when it is coupled with Kirchhoff’s two laws, we have a sufficient, powerful set of tools for analyzing a large variety of electric circuits. Kirchhoff’s laws were first introduced in 1847 by the German physicist Gustav Robet Kirchhoff (1824-1887). These laws are formally known as Kirchhoff’s current law (KCL) and Kirchhoff’s voltage law (KVL).
Kirchhoff’s first law is based on the law of conservation of charge, which requires that the algebraic sum of charges within a system cannot change.
Kirchhoff’s current law (KCL) states that the algebraic sum of currents entering a node (or a closed boundary) is zero.
Mathematically, KCL implies that
Where N is number of branches connected to the node and in is nth current entering (or leaving) the node. By the law, current entering a node may be regarded as positive, while currents leaving the node may be taken as negative or vice versa.
To prove KCL assume a set of currents , k = 1, 2 … flow into a node. The algebraic sum of currents at the node is
Integrating both sides of [link] gives
Where and but the law of conservation of electric charge requires that the algebraic sum of electric charges at the note must not change; that is, the node stores no net charge. Thus , confirming the validity of KCL.
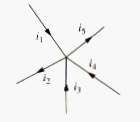
Consider the node in [link]. Applying KCL gives
Since current , and are entering the node, while current and are leaving it. By rearranging the terms, we get
[link] is an alternative form of KCL:
The sum of the current entering a node is equal to the sum of the currents leaving the node.
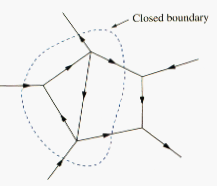
Note that KCL also applies to a closed boundary. This may be regarded as generalized case, because a node may be regarded as a closed surface shrunk to a point. In two dimensions, a closed boundary is the same as a closed path. As typically illustrated in the circuit of [link], the total current entering the closed surface is equal to the total current leaving the surface.
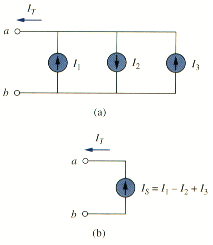
A simple application of KCL is combining current sources in parallel. The combined current is the algebraic sum of the current supplied by the individual sources. For examples, the current sources shown in [link](a) can be combined as in [link](b). The combined or equivalent current source can be found by applying KCL to node a.
or
A circuit cannot contain two different currents, and , in series, unless ; otherwise KCL will be violated.
Kirchhoff’s second law is based on the principle of conservation of energy:
Kirchhoff’s voltage law (KVL) states that the algebraic sum of all voltages around a closed path (or loop) is zero.
Expressed mathematically, KVL states that
Where M is the number of voltages in the loop (or the number of branches in the loop) and vm is the mth voltage.
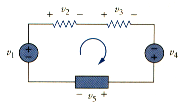
To illustrate KVL, consider the circuit in [link]. The sign on each voltage is the polarity of the terminal encountered first as we travel around the loop. We can start with any branch and go around the loop either clockwise or counterclockwise. Suppose we start with the voltage source and go clockwise around the loop as shown; then voltages would be , , , , and , in that order. For example, as we reach branch 3, the positive terminal is met first; hence we have . For branch 4, we reach the negative terminal first; hence, . Thus, KVL yields
Rearranging terms gives
Which may be interpreted as
Sum of voltage drops = sum of voltage rises
This is an alternative form of KVL. Notice that if we had traveled counterclockwise, the result would have been , , , , and , which is the same as before except that the sign are reversed. Hence, [link] and [link] remain the same.
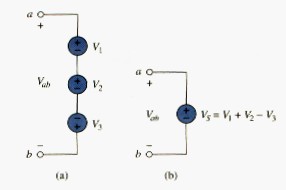
When voltage sources are connected in series, KVL can be applied to obtain the total voltage. The combined voltage is the algebraic sum of the voltage of the individual sources. For example, for the voltage shown in [link](a), the combined or equivalent voltage source in [link](b) is obtained by applying KVL.
or
To avoid violating KVL, a circuit cannot contain two different voltages and in parallel unless .
SERIES RESISTORS AND VOLTAGE DIVISION
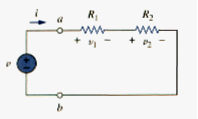
The need to combine resistors in series or in parallel occurs so frequently that it warrants special attention. The process of combining the resistors is facilitated by combining two of them at a time. With this in mind, consider the single-loop circuit of [link] the two resistors are in series, since the same current i flows in both of them. Applying Ohm’s law to each of the resistors, we obtain
and
If we apply KVL to the loop (moving in the ckockwise direction), we have
Combining [link] and [link], we get
or
Notice that [link] can be written as
implying that the two resistors can be replaced by an equivalent resistor ; that is
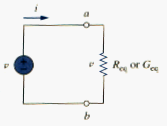
Thus, [link] can be replaced by the equivalent circuit in [link]. Two circuits in [link] and [link] are equivalent because they exhibit the same voltage-current relationship at the terminals a-b. An equivalent circuit such as the in [link] is useful in simplying the analysis of a circuit. In general,
The equivalent resistance of any number of resistors connected in series is the sum of the individual resistance.
For N resistors in series then,
To determine the voltage across each resistor in [link], we substitute [link] into [link] and obtain
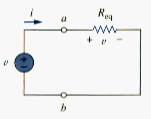
Note that the voltage v is divided among the resistor in direct proportion to their resistances; the larger the resistance, the larger the voltage drop. This is called the principle of voltage division, and the circuit in [link] is called a voltage divider. In general, if a voltage divider has N resistors ( , , ) in series with the source voltage v, the nth resistor ( ) will have a voltage drop of
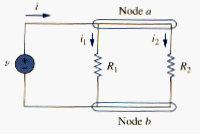
PARALLEL RESISTORS AND CURRENT DIVISION
Consider the circuit in [link], where two resistors are connected in parallel and therefore have the same voltage across them. From Ohm’s law,
or
Applying KCL at node a gives the total current I as
i = i1 + i2
Substituting [link] into Equation (34), we get
where is the equivalent resistance of the resistors in parallel:
Or
Or
Thus,
The equivalent resistance of two parallel resistors is equal to the product of their resistance divided by their sum.
It must be emphasized that this applies only to two resistors in parallel. From [link], if , then .
We can extend the result in [link] to the general case of a circuit with N resistors in parallel. The equivalent resistance is
Note that is always smaller than the resistance of the smallest resistor in the parallel combination. If , then
For example, if four 100 resistors are connected in parallel, their equivalent resistance is 25 .
It is often more convenient to use conductance rather than resistance when dealing with resistors in parallel. From [link], the equivalent conductance for N resistors in parallel is
Where , , , … . [link] states:
The equivalent conductance of resistors connected in parallel is the sum of their individual conductances.
This means that we may replace the circuit in [link] with that in [link]. Notice the similarity between [link] and [link]. The equivalent conductance of parallel resistors is obtained the same way as the equivalent resistance of resistors in series is obtained just the same way as the resistance of resistors in parallel. Thus the equivalent conductance Geq of N resistors in series (such as shown in [link]) is
Given the total current i entering node a in [link], how do we obtain current and ? We know that the equivalent resistor has the same voltage, or
Combining [link] and [link] results in
and
Which shows that the total current i is shared by the resistor in inverse proportion to their resistances. This is known as the principle of current division, and the circuit in [link] known as a current divider. Notice that the larger current flows through the smaller resistance.
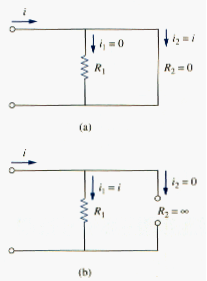
As an extreme case, suppose one of the resistors in [link] is zero, say ; that is, is a short circuit, as shown in [link](a). From [link], implies that , . this means that the entire current i bypasses and flows through the short current , the path of least resistance. Thus when a circuit is short circuited, as shown in [link](a), two things should be kept in mind:
1. The equivalent resistance . [See what happens when in [link].}
2. The entire current flows through the short circuit.
As another extreme case, suppose , that is R2 is an open circuit, as shown in [link](b). The current still flows through the path of least resistance, . By taking the limit of [link] as , we obtain in this case.
If we divide both the numerator and denominator by , [link] becomes
Thus, in general, if a current divider has N conductors ( , , …, ) in parallel with the source current i, the nth conductor ( ) will have current
In general, it is often convenient and possible to combine resistors in series and parallel and reduce a resistive network to a single equivalent resistance . Such a single equivalent resistance is the resistance between the designated terminals of the network and must exhibit the same i-v characteristics as the original network at the terminals.
WYE-DELTA TRANSFORMATIONS
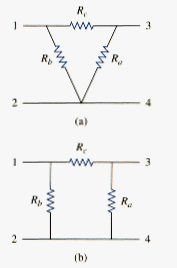
Situations often arise to circuit analysis when the resistors are neither in parallel nor in series. For example, consider the bridge circuit in [link]. How do we combine resistors through when the resistors are neither in series nor in parallel? Many circuits of the types shown in [link] can be simplified by using three terminal equivalent networks. There are the wye (Y) or tee (T) network shown in [link] and the delta ( ) or pi ( ) network shown in [link]. These networks occur by themselves or as part of a larger network. They are used in three phase networks, electrical filters, and matching network. Our main interest here is in how to identify them when they occur as part of a network and how to apply wye-delta transformation in the analysis of that network.
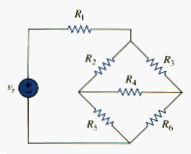
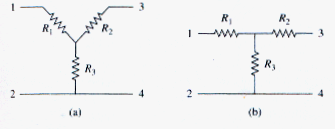
Delta to wye conversion
Suppose it is more convenient to work with a wye network in a place where the circuit contains a delta configuration. We superimpose a wye network on the existing delta network and find the equivalent resistances in the wye network. To obtain the equivalent resistances in the wye network, we compare the two networks and make sure that the resistance between each pair of nodes in the (or ) network is the same as the resistance between the same pair of nodes in the Y (or T) network. For terminals 1 and 2 in [link] and [link], for example,
Setting gives
Similarly,
Subtracting [link] from [link]. We get
Adding [link] and [link] gives
and subtracting [link] from [link] yields
Subtracting [link] from [link]. We obtain
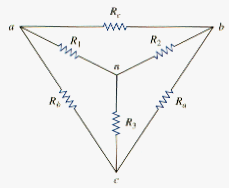
We do not need to memorize [link] to [link]. To transform a network to Y, we create extra node n as shown in [link] and follow this conversion rule:
Each resistor in the Y network is the product of the resistors in the two adjacent branches, divided by the sum of the three resistors.
One can follow this rule and obtain [link] to [link] from [link].
Wye to delta conversion
To obtain the conversion formulas for transforming a wye network to an equivalent delta network, we note from [link] to [link] that
Dividing [link] by each of [link] to [link] leads to the following equations:
From [link] to [link] and [link], the conversion rule for Y to is as follows:
Each resistor in the network is the sum of all possible products of Y resistors taken two at a time, divided by the opposite Y resistor.
The Y and networks are said to the balanced when
and
Under these conditions, conversion formulas become
or
One may wonder why is less than . Well, we notice that the Y-connection is like a “series” connection while the -connection is like a “parallel” connection.
Note that in making the transformation, we do not take anything out of the circuit or put in anything new. We are merely substituting different but mathematically equivalent three-terminals network patterns to create a circuit in which resistors are either in series or in parallel, allowing us to calculate if necessary.
SUMMARY
- A resistor is a passive element in which the voltage v across it is directly proportional to the current I through it. That is, a resistor is a device that obeys Ohm’s law,
V = iR
where R is resistance of the resistor.
- A short circuit is a resistor (a perfectly conducting wire) with zero resistance (R = 0). An open circuit is a resistor with infinite resistance (R = ).
- The conductance G of a resistor is the reciprocal of its resistance:
- A branch is a single two-terminal element in electric circuit. A node is the point of connection between two or more branches. A loop is closed path in a circuit. The number of branches b, the number of the node n, and the number of independent loops l in a network are related as
b = l + n - 1
- Kirchhoff’s current law (KCL) states that the currents at any node algebraically sum to zero. In other words, the sum of the currents entering a node equals the sum of currents leaving the node.
- Kirchhoff’s voltage law (KVL) states that the voltages around closed path algebraically sum to zero. In other words, the sum of the voltage rises equals the sum of the voltage drops.
- Two elements are in series when they are connected sequentially, end to end. When elements are in series, the same current flows through them ( ). They are in parallel if they are connected to the same to nodes. Elements in parallel always have the same voltage across them ( ).
- When two resistors and are in series, their equivalent resistance and equivalent conductance are
,
- When two resistors and are in parallel, their equivalent resistance and equivalent conductance are
,
- The voltage division principle for two resistors in series is
,
11. The current division principle for two resistors in parallel is
,
- The formulas for a delta-to-wye transformation are
, ,
- The formulas for a wye-to-delta transformation are
, ,